86. Soluzioni del 20 marzo 2023 – Matematica Senza Frontiere

Soluzioni del 20 marzo 2023 a cura di Fabio Ciuffoli

Ieri abbiamo presentato quattro giochi tratti dal sito web Matematica Senza Frontiere (MSF) per studenti delle classi seconde e terze delle scuole superiori. Sono arrivate sul blog numerose e ottime soluzioni sia algebriche che grafiche. Siamo sempre più orgogliosi dei nostri lettori. In ogni caso,  pubblichiamo di seguito le nostre proposte di soluzione.

Matematica Senza Frontiere – soluzioni 

1. Nella classe 3B composta da 24 alunni il professore di matematica, che si ritiene un esperto nel calcolo delle probabilità, individua l’alunno da interrogare nel modo seguente. Apre a caso un libro di 200 pagine, legge il numero della pagina e interroga l’alunno indicato sul registro col numero corrispondente. Se il numero della pagina è superiore a 24, allora, il professore procede sommando le singole cifre della pagina selezionata. Al numero ottenuto corrisponderà, sul registro di classe, il nominativo del fortunato.

Carlo, numero 3 nell’elenco, ritiene che questo sistema non garantisca a tutti gli alunni la stessa probabilità di essere chiamati; secondo i suoi calcoli, infatti, avrebbe una probabilità pari a 4 volte quella della sua amica del cuore, Franca, a cui corrisponde il numero 20.

A) Carlo ha ragione?

Luisella, numero 11, ritiene, invece, di essere lei la più sfortunata in quanto, dai suoi calcoli avrebbe una probabilità, di essere chiamata dal terribile professore, maggiore di quella di Carlo.

B) Luisella ha ragione?

1. SOLUZIONE. A) Le pagine favorevoli per Carlo sono: 3, 30, 102, 111, 120, quindi 5 su 200. La pagina favorevole per Franca è solo la n. 20, quindi 1 su 200. Carlo ha ragione a ritenersi più sfavorito rispetto a Franca, ma con una probabilità non quadrupla, bensì quintupla.

B) Le pagine favorevoli per Luisella sono 11, 29, 38,47 ,56, 65, 74, 83, 92, 119, 128, 137, 146, 155, 164, 173, 182, 191, quindi 18 su 200. Luisella ha ragione perché ha più del triplo di probabilità di essere chiamata rispetto a Carlo.

2. La scorsa estate Matthew si è recato in Giappone per un viaggio di lavoro. All’andata è partito dall’aeroporto di Londra alle 19:25 del 19 luglio ed è atterrato a Tokyo alle 17:25 del 20 luglio. Per il viaggio di ritorno, invece, è partito alle 08:50 del 25 luglio, atterrando a Londra alle 15:50 dello stesso giorno. Il volo di andata è durato un’ora in meno del volo di ritorno.

Calcolare la durata di ciascun volo e quanti fusi orari ci sono tra Tokyo e Londra.

2. SOLUZIONE. Indichiamo con V la durata del volo di ritorno e con F il fuso orario tra Tokyo e Londra, considerando gli orari di partenza e di arrivo dei due voli, si ha: V – 1 + F = 22 e V – F = 7. Risolvendo il sistema si ottiene V = 15 ore e F = 8 ore, quindi la durata del volo di andata = 14 ore. Riassumendo: volo di andata 14 ore; volo di ritorno 15 ore; fuso orario 8 ore. La differenza della durata dei voli di andate e ritorno è dovuta alla rotazione terrestre e al diverso attrito che l’atmosfera esercita sul aereo. Londra nel mese di luglio adotta l’ora legale (DST + 1) al contrario di Tokyo che adotta l’ora solare.

3. La figura seguente è un rettangolo costituito da 13 quadrati. Le lunghezze dei lati dei quadrati sono, in millimetri, numeri interi tutti differenti. Alcune sono riportate sula figura. Determinare la lunghezza dei lati degli altri quadrati.

(Il disegno non è in scala).

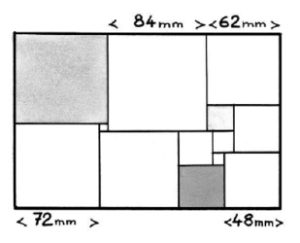
3. SOLUZIONE. La difficoltà di questo problema è l’individuazione del primo quadrato di cui sia opportuno trovare la misura del lato. Ecco una possibile soluzione.

• Il quadrato 1 ha un lato di 22 mm (84 – 62).
• Il quadrato 2 ha un lato di 40 mm (62 – 22).
• Il quadrato 3 ha un lato di 78 mm (62 + 40 + 48 – 72).
• Il quadrato 4 ha un lato di 6 mm (78 – 72).
• Il quadrato 5 ha un lato di 18 mm (40 – 22).
• Il quadrato 6 ha un lato di 10 mm (40 + 18 – 48).
• Il quadrato 7 ha un lato di 28 mm (18 + 10).
• Il quadrato 8 ha un lato di 38 mm (10 + 28).
• Il quadrato 9 ha un lato di 66 mm (28 + 38).

4. Si tagli un quadrato secondo due rette perpendicolari in quattro pezzi identici. Questi quattro pezzi possono essere disposti in modo da formare un quadrato più grande con un buco quadrato al centro. A partire da un quadrato di 8 cm di lato, effettuate tale procedimento in modo che le 5 regioni del quadrato grande abbiano la stessa area. Disponete i quattro pezzi ritagliati formando il grande quadrato a destra. Calcolare i valori delle lunghezze dei quattro lati dei pezzi ritagliati.

4. SOLUZIONE. Poiché l’area del quadrato di lato 8 cm è di 64 cm², l’area di ognuna della 4 parti misura 16 cm² come, quindi, l’aera del buco quadrato centrale nel secondo quadrato grande. Il suo lato misura 4 cm.

Indichiamo con x e y le due parti del lato del quadrato, avremo: x + y = 8 cm e x – y = 4 cm, da cui si ottiene x = 6 cm e y = 2 cm.

L’area complessiva del quadrato grande è 80 cm² (16 + 64) quindi le quattro parti uguali hanno i due lati uguali pari a √80/2 = 2 √5 cm.

A lunedì prossimo.