Menu
Le soluzioni dell’8 novembre 2021 a cura di Fabio Ciuffoli
Ieri mattina abbiamo pubblicato il gioco della scacchiera e ora presentiamo le soluzioni.
Una fiera di paese e una scacchiera quadrata – soluzioni
A una fiera di paese, i giocatori lanciano una moneta su una larga scacchiera quadrata. Se la moneta si ferma sul bordo di una casella, il giocatore perde. Se la moneta rotola fuori dalla scacchiera viene restituita al giocatore. Se la moneta cade all’interno di una casella si restituisce la moneta al giocatore che vince anche un premio. I lati della scacchiera sono 60 cm, su ogni lato vi sono sei file larghe 10 cm ciascuna e la moneta ha un diametro di 6 cm.
1. Qual è la probabilità di vincere per un giocatore?
2. Un giocatore, dopo aver perso diverse partite, vi chiede: “Quale dimensione dovrebbe avere, il diametro della moneta, per rendere il gioco con una probabilità di vincita del 50%?”.
SOLUZIONE. 1. Ipotizziamo che la scacchiera sia costruita a secco su un tavolo rialzato quadrato 60×60 quindi se il centro della moneta si venisse a trovare fuori dalla scacchiera, la moneta cadrebbe e il gioco si sarebbe in parità. Per risolvere questo problema, calcoliamo le probabilità in riferimento ad una superficie campione di un solo quadrato. Per vincere, il centro della moneta deve fermarsi ad almeno 3 cm di distanza da ogni lato. In altri termini il centro della moneta deve cadere all’interno del quadrato grigio, altrimenti la moneta si ferma al di fuori della casella, come disegnato in figura.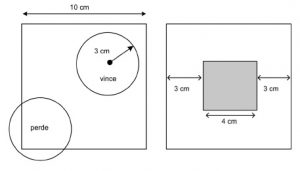 
Il problema viene così riformulato: calcolare la probabilità che il centro, di una moneta dal diametro di 6 cm, cada in un quadrato di lato 4 cm, interno a un quadrato di lato 10 cm. La probabilità, che il centro della moneta cada nel quadrato grigio, è data dal rapporto tra l’area del quadrato grigio e l’area del quadrato della scacchiera, 16 su 100. La probabilità di vincere è quindi 16%/.
2. Per rendere il gioco equiprobabile, con probabilità del 50%, l’area del quadrato grigio dovrà essere la metà dell’area del quadrato di lato 10 cm. Definendo x il lato del quadrato grigio, avremo x²/100 = 50/100. Svolgendo x = √ 50 = 7,07 cm. Il diametro della moneta dovrà essere quindi di 10 – 7,07 = 2,93 cm.
Diverso sarebbe il risultato, se ipotizzassimo che la scacchiera fosse disegnata a livello del piano, ad esempio su un bancone o sulla strada, quindi con la presenza di aree laterali. In questo caso, anche se il centro della moneta venisse a trovarsi fuori dalla scacchiera, la moneta potrebbe coprire il bordo facendo risultare perdente il giocatore. In questa seconda ipotesi i risultati sarebbero: 13,25% e 2,62 cm.
Entrambe le ipotesi sono ammesse dal testo del problema, che non indica precisamente se si tratta di un tavolo rialzato o di un disegno su una superficie più ampia.
Un buon modo per ragionare a partire da ipotesi differenti!
In copertina Fiera di San Martino di Giuseppe Boschetti. A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Abbiamo ricevuto diverse proposte di soluzione, con procedure molto interessanti, in particolare sull’ipotesi della scacchiera in piano. Vorrei qui segnalarne almeno due e ringraziare gli autori.
Giuseppe Roccasanta sul questo blog ha scritto “… affinché la moneta cada dentro il quadrato o tocchi il bordo dello stesso, dobbiamo considerare che il centro della moneta cada dentro il quadrato oppure entro una fascia perimetrale che genera un quadrato con gli angoli arrotondati. Chiamiamo l il lato del singolo quadratino della scacchiera, n il numero di quadratini per ogni lato, e r il raggio della moneta. L’area di questa fascia perimetrale sarà: [4 * ( l * n * r )] + ( r^2 * π ) . L’area della scacchiera sarà: ( l * n )^2. Affinché la moneta cada dentro uno dei quadratini della scacchiera senza toccare il bordo bisogna che cada dentro un quadrato concentrico al quadratino della scacchiera la cui area è: [ l – ( 2 * r )]^2 . Quindi l’area utile sarà: n^2 * [( l – ( 2 * r )]^2 .
La probabilità è data dall’area utile diviso l’area totale (area della scacchiera più la fascia perimetrale):
n^2 * [( l – (2 * r )]^2
––––––––––––––––––––––––––––––––
( l * n )^2 + (4 * l * n * r ) + (r^2 * π)
Andando a sostituire con le misure indicate si ottiene una probabilità del 13,2466%.
Con lo stesso ragionamento, per portare la probabilità al 50% dobbiamo porre l’area utile uguale alla metà dell’area totale:
6^2 * [( 10 – ( 2 * r )]^2 = [( 10 * 6 )^2 + (4 * 10 * 6 * r) + ( r^2 * π )] / 2
Svolgendo in r e risolvendo l’equazione di secondo grado si ottiene un diametro di 2,62 circa.
Alessandro Pettinelli ha scritto “… indicando con d il diametro della moneta e p la probabilità di vincita del giocatore, ti allego le formule generali per il calcolo di p noto d e di d noto p. [che riporto in fotografia jpg].
Grazie per la collaborazione.