
12. I giochi del lunedì di Prisma 27 settembre 2021 a cura di Fabio Ciuffoli
Proponiamo oggi un gioco prendendo spunto dall’inaugurazione dell’anno scolastico in Russia. Invitiamo i lettori a presentarci osservazioni e proposte di soluzione nello spazio riservato ai commenti. Alle ore 17.00 di domani pubblicheremo la soluzione.
Il primo ministro russo risolve un problema di geometria
Agli inizi di queso mese, il primo ministro russo Mikhail Mishustin ha celebrato il Giorno del Sapere, visitando una delle migliori scuole del suo paese nei pressi di Mosca.
Terminato il discorso inaugurale, si è avvicinato alla lavagna e ha proposto il seguente problema:
“A partire da un punto su una circonferenza, siete in grado di disegnare una perpendicolare al diametro, senza utilizzare dispositivi di misurazione?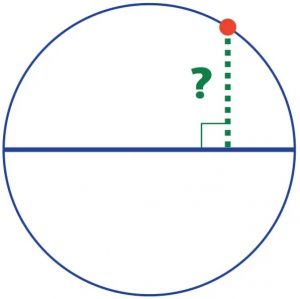
La bellezza di questo problema è nella restrizione degli strumenti di misurazione. E’ permesso solo un righello, non contrassegnato, per disegnare linee rette.
La fotografia del primo ministro, in alto, fornisce qualche indizio. Ad esempio l’angolo inscritto in una semicirconferenza è retto. Alcune conoscenze sui triangoli possono essere utili: l’altezza di un triangolo è il segmento che parte da un vertice e forma un angolo retto incontrando il lato opposto; nei triangoli acuti le tre altezze si intersecano sempre.
Mi è sembrato strano, ma interessante, che un politico tra i più potenti della Russia abbia usato la geometria per comunicare coi ragazzi e con la popolazione. Non capita tutti i giorni di vedere un politico, da qualsiasi paese provenga, scrivere un problema stimolante di matematica su una lavagna e risolverlo.
Per completezza, va anche detto che il governo russo è stato criticato dalla comunità matematica internazionale per le violazioni dei diritti umani contro il matematico e anarchico Azat Miftakhov, condannato a sei anni in una colonia penale all’inizio di quest’anno per presunto teppismo. Una petizione per la sua scarcerazione, alla quale ha aderito anche l’Unione Matematica Italiana, è stata firmata da più di 3000 matematici accademici di tutto il mondo.
Aggiornamento per le soluzioni click qui
Si ringrazia l’International Congress of Mathematicians (ICM) per l’utilizzo delle immagini.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
13 Responses
Credo esista una soluzione più semplice di quella proposta da Aurelio (ma le mie scarse competenze in geometria mi fanno dubitare che sia corretta).
1) scelgo un punto qualunque della circonferenza.
2) traccio un triangolo che unisca i due estremi del diametro al punto casuale che ho scelto.
3) misuro i 3 lati e li uso per calcolare l’altezza
4) uso la misura dell’altezza (che ancora non so dove deve “cadere” sul diametro, ma so quanto è lunga) insieme a uno dei lati per idealizzare un nuovo triangolo, rettangolo, composto anche da una “porzione” del diametro.
5) a questo punto uso altezza e lato per misurare con il teorema di Pitagora la lunghezza della porzione di diametro.
6) segno il punto della lunghezza ottenuta con il passaggio 5 sul diametro.
7) unisco il punto trovato sul diametro al punto casuale scelto all’inizio… e quella linea sarà perpendicolare al diametro
Sbaglio o è fattibile?
La soluzione proposta non rispetta i vincoli del problema. Si puó usare solo un righello non numerato quello che una volta si chiamava “asta”.
Scusate non avevo letto bene.
Avevo capito di poter usare solo un righello, ma non solo un righello non segnato!
Mi arrendo!
Sarebbe bello sapere se uno dei nostri ministri saprebbero risolvere un problema geometrico solo col righello!!
Domanda con risposta difficile, ma se una persona si prepara, come avrà fatto il primo ministro russo, credo sia possibile. È interessante la scelta del problema e l’uso della lavagna, che ricorda la geometria dell’antica Grecia.
Bravo Aurelio Roccasanta
Ottimo. La soluzione del
Primo Ministro è più complessa e allora mi chiedo se con un semplice righello si puó tracciare la tangente a un cerchio?
Salve,
ecco la mia soluzione:
Traccio una retta passante per un estremo del diametro (che chiamo A, L’altro estremo lo chiamo B) e il punto da me scelto (che chiamo P) , dopodiché partendo da P traccio la tangente a esso che per forza di cose interseca il diametro ( in un punto che chiamo I) a questo punto partendo da I traccio la tangente che dà sull’altro semicerchio (il punto con cui interseca la circonferenza lo chiamo Q), poi unisco P e Q e così ottengo un segmento perpendicolare al diametro (e che lo interseca nel punto L).
Per dimostrare che è perpendicolare utilizzo il teorema delle tangenti e delle secanti secondo il quale posso scrivere le relazioni sulle 2 tangenti che intersecano entrambe la secante AB:
AI : PI = PI : BI
AI : QI = QI : BI
tramite sostituzione ottengo
PI^2/BI*QI= QI/BI
e quindi:
PI^2/BI= QI^2/BI
semplifico BI e metto sotto radice i due membri così da ottenere:
PI = QI
a questo punto siccome i 2 segmenti sono due lati di un triangolo isoscele(è iloscele perchè ha due lati uguali) con base PQ posso dire che gli angoli alla base sono uguali, ovvero:
PQI = QPI
A questo punto posso dire che i due triangoli PLI e QLI sono uguali perchè hanno un lato uguale(PI e QI), un angolo uguale (PQI e QPI) e infine hanno un lato in comune che è LI.
Siccome i 2 triangoli sono sono uguali allora posso dire che:
QIL = PIL
ora considerato che la somma degli angoli interni di un triangolo fa sempre 180 posso dire (riferendomi al triangolo PQI) che:
QIP + PQI + QPI = 180
siccome PQI e QPI sono uguali perchè i triangoli PLI e QLI sono congruenti, e considerato che QIP=PIL+QIL e quindi QIP=2QIL sotituisco:
QIP + PQI + QPI = 180
in:
2QIL + 2LQI = 180
Divido tutto per 2:
QIL + LQI = 90
a questo punto siccome la somma degli angoli interni del triangolo QIL deve essere 180 e che la somma tra gli angoli QIL e LQI fa 90 allora l’angolo QLI deve misurare 180- (QIL LQI)= 180-90= 90.
Ora siccome QLI= PLI allora anche PLI=90
Avendo dimostrato che QLI e PLI sono uguali a 90 gradi possiamo affermare con certezza che il segmento PQ è una perpendicolare sul diametro visto che l’angolo risultante dall’intersezione dei 2 segmenti misura 90 gradi.
Aurelio ti chiedo gentilmente se riesci a inserire un disegno immagine o foto nei formati supportati dal sito. In questo modo sarà più facile leggere la tua soluzione e coinvolgere anche altri lettori. Comunque me lo studio con calma. A presto
C’ho dovuto ragionare ma alla fine sono riuscito a capire la soluzione… credo…
Funziona perché I è un punto dipendente dalla casualità di P giusto?
Se I fosse stato fissato all’inizio dell’indovinello, sarebbe stato possibile usarlo per dedurre P e fare poi lo stesso ragionamento?
Ottimo. Oggi pomeriggio la soluzione con i disegni.
Costruzione con riga e compasso? oppure il compasso è vietato?
Compasso non ammesso. Si può usare solo un righello, non numerato, per tracciare linee.