Menu
Le soluzioni dell’11 marzo 2024 a cura di Fabio Ciuffoli
Ieri abbiamo presentato quattro problemi, considerati degli evergreen del problem solving, sempre stimolanti e suggestivi. I primi due sono sulla sulla dissezione e l’assemblaggio e il terzo e il quarto sulla lunghezza di una corda avvolta attorno a un cilindro. Di seguito pubblichiamo le nostre proposte di soluzione.
Un quadrato e un cilindro con la corda attorno
1. Un falegname vuole ottenere una tavola di legno quadrata che misura 60 cm per 60 cm, ma nel suo laboratorio ha solo una tavola rettangolare di 50 cm per 72 cm. Come è possibile tagliare il legno in due pezzi, in modo che possano essere incollati insieme, per formare la tavola quadrata desiderata?
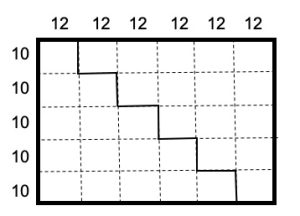
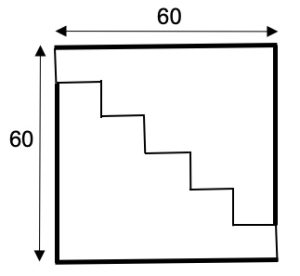
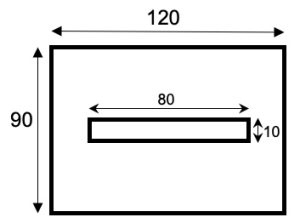
2. SOLUZIONE. Si taglia la tavola rettangolare, come proposto in figura seguente, poi il pezzo di destra viene spostato di 10 cm in basso e di 20 cm a sinistra. in modo da formare un quadrato di lato 100 cm. Anche in questo caso, come in quello precedente, si può ragionare partendo dalla superficie totale 120 * 90 – 80 * 10 = 10.000 cm2 e via di seguito.
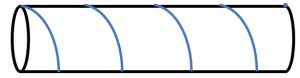
3. SOLUZIONE. Il problema sembra molto complicato, in realtà occorre solo una piccola intuizione e la conoscenza del teorema di Pitagora. Immaginiamo un cilindro di cartone da cucina e tagliamolo lungo la sua altezza dai punti in cui si trovano le estremità della corda. Quando lo srotoliamo, otteniamo un rettangolo di 24 cm per 8 cm, come illustrato in figura.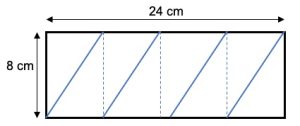
Il rettangolo grande è diviso in quattro rettangoli di uguali dimensioni, 6 cm x 8 cm e con Pitagora possiamo calcolare la lunghezza dell’ipotenusa, che indichiamo con x. Avremo x2 = 62 + 82 da cui x = 10 cm. Infine, la lunghezza totale della corda è pari a quattro ipotenuse, quindi 4 x 10 = 40 cm.
4. Una corda è avvolta regolarmente intorno a un cilindro di diametro 14 cm compiendo tre giri completi. Il primo giro si completa a 10 cm dalla base, il secondo giro si completa a 20 cm dal primo e il terzo a 30 cm dal secondo, come disegnato in figura. Quanto è lunga la corda?
4. SOLUZIONE. Anche in questo caso, sviluppiamo il cilindro ottenendo un rettangolo di base 60 cm e di altezza 14π. La lunghezza della corda è data dalla somma delle ipotenuse dei tre triangoli rettangoli, di base rispettivamente 10, 20 e 30 e di altezza 14π, che corrisponde a circa 146,69 cm.
I Giochi del Lunedì tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).