Menu
I Giochi del Lunedì di Prisma del 20 marzo 2023 a cura di Fabio Ciuffoli
Oggi proponiamo 4 problemi che hanno fatto parte delle prove di preparazione ai giochi internazionali di Matematica Senza Frontiere (MSF) svolte la settimana scorsa, per studenti delle classi seconde e terze delle scuole superiori. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio relativo ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
Matematica Senza Frontiere
1. Nella classe 3B composta da 24 alunni il professore di matematica, che si ritiene un esperto nel calcolo delle probabilità, individua l’alunno da interrogare nel modo seguente. Apre a caso un libro di 200 pagine, legge il numero della pagina e interroga l’alunno indicato sul registro col numero corrispondente. Se il numero della pagina è superiore a 24, allora, il professore procede sommando le singole cifre della pagina selezionata. Al numero ottenuto corrisponderà, sul registro di classe, il nominativo del fortunato.
Carlo, numero 3 nell’elenco, ritiene che questo sistema non garantisca a tutti gli alunni la stessa probabilità di essere chiamati; secondo i suoi calcoli, infatti, avrebbe una probabilità pari a 4 volte quella della sua amica del cuore, Franca, a cui corrisponde il numero 20.
A) Carlo ha ragione?
Luisella, numero 11, ritiene, invece, di essere lei la più sfortunata in quanto, dai suoi calcoli avrebbe una probabilità, di essere chiamata dal terribile professore, maggiore di quella di Carlo.
B) Luisella ha ragione?
2. La scorsa estate Matthew si è recato in Giappone per un viaggio di lavoro. All’andata è partito dall’aeroporto di Londra alle 19:25 del 19 luglio ed è atterrato a Tokyo alle 17:25 del 20 luglio. Per il viaggio di ritorno, invece, è partito alle 08:50 del 25 luglio, atterrando a Londra alle 15:50 dello stesso giorno. Il volo di andata è durato un’ora in meno del volo di ritorno.
Calcolare la durata di ciascun volo e quanti fusi orari ci sono tra Tokyo e Londra.
3. La figura seguente è un rettangolo costituito da 13 quadrati. Le lunghezze dei lati dei quadrati sono, in millimetri, numeri interi tutti differenti. Alcune sono riportate sula figura. Determinare la lunghezza dei lati degli altri quadrati.
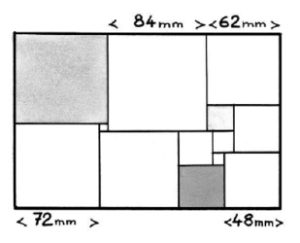(Il disegno non è in scala).
4. Si tagli un quadrato secondo due rette perpendicolari in quattro pezzi identici. Questi quattro pezzi possono essere disposti in modo da formare un quadrato più grande con un buco quadrato al centro. A partire da un quadrato di 8 cm di lato, effettuate tale procedimento in modo che le 5 regioni del quadrato grande abbiano la stessa area. Disponete i quattro pezzi ritagliati formando il grande quadrato a destra. Calcolare i valori delle lunghezze dei quattro lati dei pezzi ritagliati.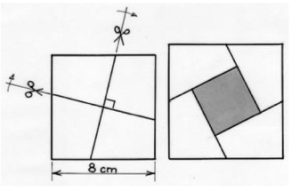
Aggiornamento per le soluzioni click qui.
I giochi sono tratti dal sito web http://www.matematicasenzafrontiere.it/msf/
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
25 risposte
Problema 3 in ordine crescente
6 10 18 22 28 38 40 66 78
Tutto espresso in mm
Problema 4 in ordine crescente
2 4 6 8 Tutto espresso in cm
Ottimo, nel pomeriggio tutte le soluzioni.
Disegno imperfetto fatto in giro.
Problema N. 4. vedi immagine
il disegno
N. 1. Nooo, ma ha troppo ragione la povera Luisella con 18 probabilità su 200! Addirittura quelli dal 20 al 24 hanno solo 1 probabilità su 200, cioè solo se esce giusta la loro pagina. I centrali sono messi molto peggio degli altri! Carlo ha solo 5 su 200, meglio che stia zitto e non si lamenti 😅. E comunque anche la scelta “casuale” della pagina, dà da pensare….no, no, metodo molto ingiusto! Sono contraria 😅😅
Hai ragione. Alle superiori alcuni prof. aprivano la pagina e facevano la somma. Il n. 1 (Andreoli) e il 28 (Zuffolini) erano praticamente al sicuro. Io ho sempre avuto numeri fra 8 e 10…😖😖
Alfonso Cornia, pensa a me che ero la 10 in classe di 20
Ciao Raffaella, ben ritrovata!😊😊
Problema n. 3 vedi immagine
Ammesso che la scelta del professore sia veramente casuale, distribuita uniformemente tra 1 e 200, Carlo viene pizzicato 5 volte su 200 nei casi 3, 30, 102, 111, 120. Franca con il numero 20 viene chiamata solo se viene aperta la pagina 20. Quindi Carlo ha una probabilità pari a 5 volte quella di Franca di essere scelto.
Luisella viene scelta 18 volte su 200 con le pagine: 11, 29, 38, 47, 56, 65, 74, 83, 92, 119, 128, 137, 146, 155, 164, 173, 182, 191. La sua probabilità è sicuramente maggiore di quella di Carlo ma è messo peggio di lei il numero 10 che ha 19 modi di essere scelto: 10, 28, 37, 46, 55, 64, 73, 82, 91, 109, 118, 127, 136, 145, 154, 163, 172, 181, 190.
P.S. Con questo criterio di scelta gli ultimi in elenco sono quelli che vengono scelti meno frequentemente. Dal numero 20 al 24 solo se viene aperta proprio la pagina corrispondente al loro numero. Io con il mio cognome ho sempre accolto di buon grado questo metodo di scelta!
A parte il fatto che, come al solito, la risposta giusta è quella di Giorgio (che saluto e cui va tutta la mia mia simpatia), il quesito poteva essere presentato in modo migliore.
Il professore di matematica che non conosce la matematica, l’esperto in probabilità che non sa neanche di cosa sta parlando, un libro per individuare un numero mediante una pagina, quando le pagine sono due: che fa, lancia una moneta per scegliere la pagina destra o la sinistra?
Il testo ha fatto parte di una prova ufficiale a livello internazionale di Matematica Senza Frontiere, per cui va preso così come è e vanno ipotizzate condizioni ideali ad esempio la pagina a destra o a sinistra del imbranato prof va scelta casualmente
Evidentemente a Matematica Senza Frontiere hanno una scarsa considerazione per i professori di matematica esperti di calcoli probabilistici perché anche un bambino è in grado di capire che 1+9+9=19 è la massima somma ottenibile con le pagine fino a 200 e che solo gli studenti con numero > 19 hanno solo 1 probabilità su 200 di essere interrogati mentre tutti gli altri ne hanno di più.
A parte il fatto che, come al solito, la risposta giusta è quella di Giorgio (che saluto e cui va tutta la mia mia simpatia), il quesito poteva essere presentato in modo migliore.
Il professore di matematica che non conosce la matematica, l’esperto in probabilità che non sa neanche di cosa sta parlando, un libro per individuare un numero mediante una pagina, quando le pagine sono due: che fa, lancia una moneta per scegliere la pagina destra o la sinistra?
Problema n°1.
•P(Carlo-n°3)=5/200=0,025→2,5%
•P(Franca-n°20)=1/200=0,005→0,5%
•P(n°21, 22, 23, 24)= =1/200=0,005→0,5%
•P(Luisella-n°11)=18/200=0,09→9%
•P(n°10)=19/200=0,095→9,5%
••Quindi Carlo ha ragione; col criterio del docente, non tutti hanno la stessa probabilità di essere giustamente scelti.
••Luisella non ha ragione del tutto; ha ragione nel dire che ha una probabilità > di quella di Carlo, ma più sfortunata di lei c’è il n°10.
Quesito 1
Se si fa un elenco di quanti sono i modi in cui un allievo può essere sorteggiato a me risulta:
3) Carlo. Ha 5 modi (3 30 102 111 120)
20) Franca. Ha 1 modo (20)
11) Luisella. Ha 18 modi
10) Anonimo(?) Ha 19 modi.
Quindi Carlo non ha detto il vero perché ha una probabilità 5 volte maggiore di Franca, non 4 volte.
Luisella ha detto in parte una cosa vera (è più scalognata di Carlo), ma in parte una cosa non vera (non è la più scalognata. Il più sfortunato è il numero 10, di cui non conosciamo il nome).
P.S. Io sul registro alle superiori avevo, quasi tutti gli anni, il numero 10…
Ottimo. A domani per la soluzione.
Quesito 2.
Viaggio Andata = 15h
Viaggio Ritorno = 14h
Fusi = 7
Ops!
Avevo confuso i dati dell’andata col ritorno.
E’ corretta la soluzione di Alfonso, qui sotto. 🙂
Problema 2.
Indico con:
d la durata del viaggio di andata (quindi il viaggio di ritorno è d+1)
f la differenza infusi orari fra le due città.
Abbiamo le due relazioni:
22 = d + f
7 = d + 1 – f
Che danno i risultati: d=14 f=8.
Quindi:
Il viaggio di andata è durato 14 ore
Il viaggio di ritorno 15 ore
La differenza tra i fusi orari è di 8 ore
Chiarissimo.
Problema 3.
Problema 4.
Area del quadrato iniziale: 8*8=64. Area del quadrato finale: 64/4*5=80. Lato del quadrato finale: sqrt(80). Lato del quadratino grigio finale: 4.
a = b = sqrt(80)/2.
c + d = 8
c = d – 4
c = 2
d = 6
Chiarissimo.