
I Giochi del Lunedì di Prisma del 16 gennaio 2023 a cura di Fabio Ciuffoli
In omaggio alla vittoria dell’Argentina ai Mondiali di Calcio 2022, presentiamo tre problemi proposti da Rodolfo Kurchan di Buenos Aires, autore di giochi matematici e logici di fama internazionale. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio relativo ai commenti. Domani alle ore 17.00 pubblicheremo le nostre proposte di soluzione.
Argentina Campione del Mondo 2022
1. Messi matematico. Sostituisci le dieci lettere della seguente somma con le dieci cifre 0,1,2, … 9, in modo che la somma sia corretta. A ogni lettera corrisponde una cifra e alla stessa lettera corrisponde la stessa cifra. Ci sono due soluzioni, trova quella con il MESSI più grande.
2. Il gioco delle quattro parti. Per ciascuna delle cinque richieste seguenti, devi dividere un quadrato in quattro parti che abbiano la stessa forma (triangoli simili, quadrati, rettangoli simili ecc.) e le loro dimensioni siano determinate dalle seguenti affermazioni:
Ecco una possibile soluzione per la prima richiesta. Il quadrato è diviso in quattro triangoli che hanno la stessa forma e le stesse dimensioni. 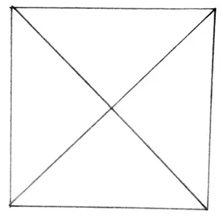
Chiarimento: per ogni richiesta, le quattro figure interne al quadrato devono essere simili (angoli corrispondenti congruenti e lati corrispondenti in proporzione) mentre le loro dimensioni possono essere le stesse o essere diverse.
3. Percorso del serpente. Il tuo obiettivo è creare un percorso di cifre in una griglia 5×5 che va 1,2,3,4,5 e poi ripetere le cifre in modo ciclico. Il percorso può iniziare da qualsiasi cella e si può spostare orizzontalmente o verticalmente, ma mai in diagonale e non può sovrapporsi. Le cifre non possono ripetersi nella stessa riga o colonna, come nel Sudoku. Ecco un esempio di percorso di lunghezza 12 a partire dall’angolo in basso a destra.
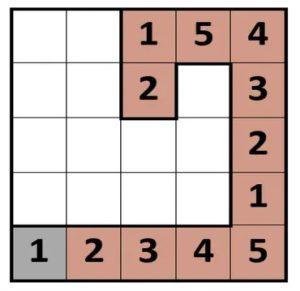
Ulteriore domanda. Qual è il percorso più lungo che puoi fare in una griglia 7×7 partendo da 1 e poi ripetendo i numeri una volta arrivato a 7?
Aggiornamento per le soluzioni click qui.
I giochi sono rielaborazione delle produzioni di Rodolfo Kurchan che ringraziamo per il lavoro svolto.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
14 risposte
Ho corretto il testo del problema 2 per renderlo più chiaro. Ho specificato che le quattro parti, in cui va diviso il quadrato, abbiano la stessa forma (triangoli simili, quadrati, rettangoli simili ecc.) e le loro dimensioni siano determinate dalle seguenti affermazioni:
Inoltre il Chiarimento: per ogni richiesta, le quattro figure interne al quadrato devono essere simili (angoli corrispondenti congruenti e lati corrispondenti in proporzione) mentre le loro dimensioni possono essere le stesse o essere diverse.
Si potrebbe lavorare, ad esempio, con opportuni rettangoli ottenuti segmentando il quadrato di partenza, ad esempio in senso verticale. Per i) basta dividere i lati opposti orizzontali in quattro parti uguali; per ii) possiamo dividere dapprima i lati predetti in cinque parti uguali: 3 rettangoli saranno congruenti, con base lunga 1/5 del lato di partenza, il quarto avrà per base il segmento restante, lungo 2/5 del lato. Per IV) si potrebbe dapprima dividere a metà il quadrato, in senso verticale e scomporre poi uno dei due rettangoli ottenuti in modo che il lato orizzontale sia la metà di quello ottenuto al primo passaggio ( quindi 2 rettangoli hanno un lato pari a 1/4 del lato del quadrato); per l’altro, si può suddividere la restante semibase secondo un rapporto differente, ad esempio 1:2. Per iii) invece si può procedere al contrario, dividendo prima il lato in questione secondo un rapporto di 1:2 ( quindi rispettivamente 1/3 e 2/3) e poi prendendo in ciascuno di essi le rispettive metà, trovando due coppie di rettangoli diversi ma tra loro congruenti. Per v) si può scegliere una partizione del lato in quattro parti non congruenti, ad esempio 1/2, 1/3, 1/10 e 1/6-1/10= 1/15.
Manca il rapporto di similitudine tra le quattro parti che compongono il quadrato. A domani per le soluzioni
È richiesta la condizione di similitudine? Pensavo bastasse solo la forma!
Propongo una risposta parziale a emendamento della precedente, introducendo la condizione di similitudine delle figure: nel caso i) e ii), il problema è risolubile con rettangoli simili.
Per i) vale ovviamente la risposta già data: quattro rettangoli congruenti verticali ciascuno con un lato corto di misura 1/4 ( posto 1 il lato del quadrato iniziale).
Per ii) la questione comincia a farsi interessante: se a, b sono le dimensioni dei tre rettangoli da supporre congruenti, il quarto rettangolo, per essere simile ai tre deve avere dimensioni ka, kb con k>0. Allora ab(3+k^2)=1 ( posto 1 il lato del quadrato, l’area deve essere unitaria), quindi ab= 1/(3+k^2). Una soluzione è data per k=3 ( per k=1, abbiamo il caso i), per k=2 otterremmo ab= 1/7, non agevole da decomporre in modo elementare): ab= 1/12= 1/3*1/4. Possiamo allora prendere i tre rettangoli congruenti pari a 1/3 di un lato ( in modo che, insieme, riempiano l’intero lato del quadrato) e 1/4 dell’altro. Ne segue che il rettangolo rimanente ha dimensioni 3/4 e 1, ed e perciò simile ai tre essendo 1/4:1/3= 3/4=3/4:1. In questo modo si trova una soluzione per rettangoli per ii) con il vincolo di similitudine.
Anche iii) si può risolvere con lo stesso metodo. Se a,b sono le dimensioni della coppia di rettangoli congruenti, allora ka, kb saranno le dimensioni dell’altra coppia di rettangoli simili alla prima. Otteniamo allora la relazione ab( 2+2k^2)=1 =>ab=1/(2+2k^2), che ha una soluzione semplice per k=2, trovando ab= 1/10= 1/2* 1/5. La prima coppia di rettangoli ha dimensioni 1/2 ( biseca il lato del quadrato) e 1/5; la seconda coppia ha lati di misura doppia della prima, quindi 1( tutto il lato del quadrato) e 2/5. La somma delle aree è 2* 1/10+ 2* 2/5= 1/5+ 4/5= 1, come richiede il problema.
Mi sembra esageratamente semplice e forse non ho compreso il quesito. Una soluzione è:
Forse non è chiarissimo nel testo, ma le quattro figure, triangoli, rettangoli o altre, devono essere simili.
La soluzione al quesito 3
Ottimo
Soluzione al quesito 1 è 92335 (la seconda è 52339)
Perfetto, a domani per le altre soluzioni.
Due triangoli non simili hanno la stessa forma? Non è richiesta la similitudine tra le 4 parti?
Forse il testo poteva precisarlo meglio, comunque nelle possibili soluzioni a me note, i triangoli sono simili. Grazie per la domanda.
Alberto Saracco Credo che nel chiarimento finale “stessa forma” è da intendere “stesso tipo di figura”.
Problema 1. 92335??