
Le soluzioni del 16 gennaio 2023 a cura di Fabio Ciuffoli
Ieri abbiamo presentato tre problemi proposti da Rodolfo Kurchan di Buenos Aires, autore di giochi matematici e logici di fama internazionale. Di seguito pubblichiamo le nostre proposte di soluzione.
Argentina Campione del Mondo 2022 – soluzioni
1. Messi matematico. Sostituisci le dieci lettere della seguente somma con le dieci cifre 0,1,2, … 9, in modo che la somma sia corretta. A ogni lettera corrisponde una cifra e alla stessa lettera corrisponde la stessa cifra. Ci sono due soluzioni, trova quella con il MESSI più grande.
1. SOLUZIONE. Cerchiamo il MESSI più grande, quindi ipotizziamo M = 9 per cui F = 1 e U = 8. Ora E + E deve essere minore di 10 (poiché se M = 9 non ci può essere riporto perché U sarebbe anch’esso 9 e ciò non è possibile) per cui E può essere 0, 2, 3, oppure 4. Possiamo eliminare E = 0, poiché ciò significherebbe che anche T sia 0 oppure 1, che sarebbe impossibile perché T deve essere diverso da E, inoltre già F = 1. Possiamo anche eliminare E = 4, poiché ciò significherebbe che T sia 8 oppure 9, che è impossibile perché sono cifre già assegnate. Quindi E = 3 oppure E = 2.
Il numero zero non può essere S, poiché anche O oppure B sarebbe zero. Il numero zero non può essere I, poiché renderebbe L zero. Né può essere T, poiché ciò darebbe un riporto alla colonna M. Inoltre possiamo considerare che zero non può essere B oppure O, poiché ciò significherebbe S = 5, che non può essere perché se S fosse 5 allora B sarebbe 1, che è già stato assegnato. Quindi L = zero, che significa I = 5.
Sappiamo che E può essere 3 oppure 2. Supponiamo E = 3, quindi T = 6 o 7. Se T = 6, allora non c’è modo di assegnare 2, 4 e 7 alle altre lettere per rendere valida l’operazione. La somma non funziona nemmeno con T = 7. Quindi E non è 3. Ora proviamo con E = 2. T deve essere 4 e infine S = 3 e O = 7 e B = 6, quindi la soluzione corretta è: 92.335 + 92.335 = 184.670. L’altra soluzione è 52.339 + 52.339 = 104.678.
2. Il gioco delle quattro parti. Per ciascuna delle cinque richieste seguenti, devi dividere un quadrato in quattro parti che abbiano la stessa forma (triangoli simili, quadrati, rettangoli simili ecc.) e le loro dimensioni siano determinate dalle seguenti affermazioni:
Ecco una possibile soluzione per la prima richiesta. Il quadrato è diviso in quattro triangoli che hanno la stessa forma e le stesse dimensioni. 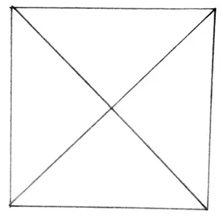
Chiarimento: per ogni richiesta, le quattro figure interne al quadrato devono essere simili (angoli corrispondenti congruenti e lati corrispondenti in proporzione) mentre le loro dimensioni possono essere le stesse o essere diverse.
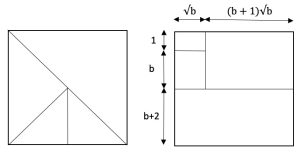
2. Soluzioni II – III – IV – V. Presentiamo le soluzioni geometriche e ricordiamo che le quattro figure interne al quadrato devono essere simili.
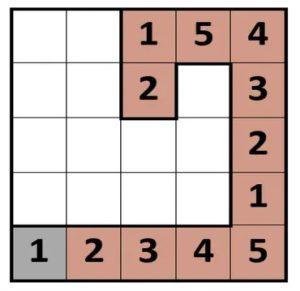
3. Percorso del serpente. Il tuo obiettivo è creare un percorso di cifre in una griglia 5×5 che va 1,2,3,4,5 e poi ripetere le cifre in modo ciclico. Il percorso può iniziare da qualsiasi cella e si può spostare orizzontalmente o verticalmente, ma mai in diagonale e non può sovrapporsi. Le cifre non possono ripetersi nella stessa riga o colonna, come nel Sudoku. Ecco un esempio di percorso di lunghezza 12 a partire dall’angolo in basso a destra.
Ulteriore domanda. Qual è il percorso più lungo che puoi fare in una griglia 7×7 partendo da 1 e poi ripetendo i numeri una volta arrivato a 7?
3. SOLUZIONE. In figura seguente un percorso con lunghezza 19.
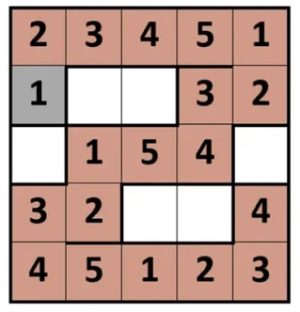
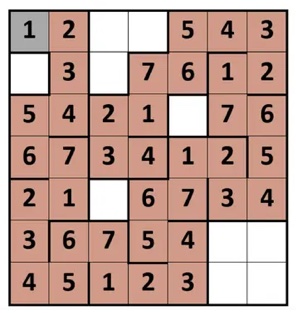
In figura seguente un percorso con lunghezza 37.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).