Menu
I Giochi del Lunedì di Prisma del 9 gennaio 2023 a cura di Fabio Ciuffoli
Oggi presentiamo sei domande che hanno fatto parte delle tanto discusse prove scritte del concorso per il reclutamento del personale docente di matematica, fisica e scienze (STEM Science, Technology, Engineering and Mathematics) nelle scuole superiori. Le prove, computer based, si sono svolte senza uso di carta e penna e con un tempo medio di circa due minuti per ciascuna risposta. Lasciamo voi le considerazioni con l’invito a inviarci osservazioni e proposte di soluzione utilizzando lo spazio dei commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
Le prove STEM per docenti
1. Sia assegnato un triangolo rettangolo di vertici A, B, C e angolo retto in A, avente perimetro di 12 cm. Nel triangolo è inscritto un cerchio di raggio uguale a 1 cm. Indicato con R il punto di tangenza tra il cerchio e il lato AB, si verifica che il segmento RB misura 3 cm. Indicato con K il punto di tangenza tra il cerchio e il lato BC, la lunghezza del segmento CK è: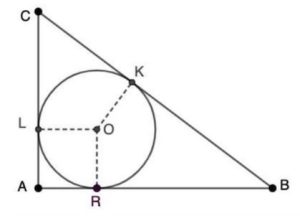
a. 2 cm b. 3 cm c. 4 cm d. (3/2) cm
2. Cecilia possiede due dadi indistinguibili con le facce numerate da 1 a 6. Uno dei due dadi è regolare, mentre l’altro è truccato; nel dado truccato, la probabilità che esca valore 1 è pari a 3/8 mentre le rimanenti facce hanno ciascuna probabilità 1/8. Qual è la probabilità che, lanciando uno dei due dadi a caso, si ottenga il valore 3?
a.15/96 b. 5/36 c. 7/48 d. 1/8
3. In un triangolo di vertici A, B e C, il lato AB misura 4 m. il lato BC 6 m. il lato CA 5. Sul lato BC si considera il punto O che dista 1 m da B. Siano A’, B’, C’ i vertici del triangolo simmetrico di ABC rispetto a O (simmetria centrale). Il perimetro del poligono non convesso ABC’A’B’C formato dal triangolo e dal suo simmetrico misura: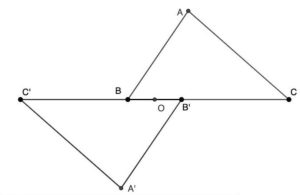
a. 30 m. b. 26 m. c. 24 m. d. 28 m.
4. Alle ultime elezioni comunali lo schieramento A ha preso il 60% dei voti mentre lo schieramento B ne ha presi il 40%. Si sa che il 50% di coloro che hanno votato lo schieramento A è favorevole all’apertura del centro storico alle auto, mentre solo il 30% di coloro che hanno votato lo schieramento B è favorevole all’apertura del centro storico alle auto. Se un elettore scelto a caso è favorevole all’apertura del centro storico alle auto, qual è la probabilità che abbia votato lo schieramento B?
a. 6/19 b. 2/7 c. 9/19 d. 3/5
5. Il raggio della circonferenza G circoscritta a un triangolo ABC è pari a 5 cm e il lato AB è lungo 6 cm. Sapendo che il punto A’, simmetrico di A rispetto al segmento BC, appartiene alla circonferenza G, l’area del quadrilatero ABA’C è pari a: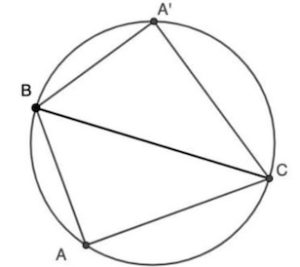
a. 48 cm2 b. 30 cm2 c. 24 cm2 d. 36 cm2
6. Sei ragazzi europei, due americani e tre africani sono gli 11 giocatori di una squadra di calcio. Sono sorteggiati a caso due di essi. Qual è la probabilità che sia sorteggiato almeno un africano?
a. 18/55 b. 11/55 c. 5/11 d. 27/55
Aggiornamento per le soluzioni click qui.
Le domande sono tratte dalle prove del Ministero dell’Istruzione – Concorso ordinario, per titoli ed esami, finalizzato al reclutamento del personale docente per i posti comuni e di sostegno della scuola secondarla di primo e secondo grado 2022.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
20 risposte
Problema sei : le condizioni determinano 3 possibilità e sono : VF,FV, VV . (F=Falso ; V=Vero)
probabilità VF= 3/11*8/10=12/55;
Probabilità FV= 8/11*3/10. =12/55;
Probabilità VV=3/11*2/10 =6/110
Sommando le tre probabilità si ha 27/55
Ottimo. Nel pomeriggio tutte le soluzioni.
1) 2cm
2) 7/48
3) 26 m
4) 2/7
5) 48 cm^2
6) 27/55
Perfetto. Nel pomeriggio le soluzioni argomentate.
Quesito 1 2 cm
Quesito 3 26 cm
Quesito 5 48 mq
Ottimo. Nel pomeriggio le altre soluzioni.
N. 5. Si risolve in 10 secondi. Il triangolo è rettangolo. Essendo l’ipotenusa pari a 10 e il cateto pari a 8, ne consegue che l’altro cateto è pari a 8. Quindi l’area del quadrilatero è 6×8 = 48.
Risultati:
1. a
2. c
3. b
4. b
5. a
6. d
Ottimo a domani per le soluzioni argomentate.
Problemino n° 1. CK=2, KB=3, in sostanza siamo nel caso di un △ r. ⇒(3, 4, 5) ⇒la prima terna pitagorica primitiva.
Problemino n° 3: ⇒2p=Perimetro ⇒⇒(ABC’A’B’C)=26 m.
Problemino n° 5: ⇒Area(▢)=2•1/2•6•√(10²–6²)=48 cm².
i problemi si risolvono effettivamente a mente in meno di due minuti cadauno (o almeno io ci ho messo massimo un minuto). Quello che mi chiedo è però quale sia l’utilità pratica per capire quali sono le competenze dei futuri insegnanti STEM in matematica. Quarto e sesto possono avere una qualche utilità, forse anche il quinto. Ma non è che fare i conti a mente sia una garanzia di sapere insegnare!
I risultati sono stati molto deludenti e si è aperto un vivace confronto tra Associazioni di categoria, Ministero ed esperti sulla efficacia delle prove ai fini della didattica. Potremmo dire, parafrasando la logica condizionale, che si tratta di competenze necessarie ma non sufficienti per un buon docente STEM.
Problema 2. La probabilità di scegliere l’uno o l’altro dado è 1/2 (perché si dice che il dado lanciato viene scelto a caso). Se si usa il primo, la probabilità che esca 3 è 1/6, se si usa il secondo essa è 1/8. In totale 1/2 * 1/6 + 1/2 * 1/8 = 1/2 * (1/6+1/8)= 1/2 * 14/48 = 7/48. La risposta corretta sembrerebbe essere la c.
Quesito 1. Se mi dicono che un triangolo rettangolo ha perimetro 12cm e devo arrangiarmi per mancanza di tempo (o anche di carta e penna come successo al concorso STEM) io parto col bias che i lati siano 3cm, 4cm, 5cm 😅
Mi sembrano veramente elementari!
Va considerato che sono computer based e sotto stress da prestazione a lungo attesa e a volte unica nella vita. In ogni caso la garanzia di selezionare buoni insegnanti è solo parziale… i risultati sono stati molto deludenti e hanno suscitato un dibattito molto acceso, ma veramente interessante, tra Ministero e associazioni di categoria.
5. Terne pitagoriche: 6^2 + 8^2 = 10^2 = (2r)^2. Quindi ABC è rettangolo di ipotenusa BC, che misura 10 cm. L’area del quadrilatero, per simmetria, è il doppio dell’area del triangolo ABC, quindi semplicemente 6*8= 48 cm^2. Risposta corretta è la (a).
Mi meraviglia che queste prove siano tanto discusse; a meno che il motivo sia per la loro elementarità.
Problema 5. BC = 2*r = 2*5 = 10
AC = sqrt(BC^2-AB^2) = sqrt(100-36) = 8
AreaTriangolo = AB*AC/2 = 6*8/2 = 24
AreaQuad = 2*AreaTriangolo = 2*24 = 48
Risposta: a)
Problema 1. RB = KB = 3, detto CK = CL = x, allora 12 = 2 * 3 + 2 * 1 + 2x, da cui x = 2