Menu
Soluzioni del 9 gennaio 2023 a cura di Fabio Ciuffoli
Ieri abbiamo presentato sei domande che hanno fatto parte delle prove scritte del concorso STEM per il reclutamento del personale docente di matematica, fisica e scienze nelle scuole superiori. Le prove, computer based, si sono svolte senza uso di carta e penna e con un tempo medio di circa due minuti per ciascuna risposta. Anche se, in generale, non sono state considerate molto difficili, in un contesto concorsuale hanno procurato qualche difficoltà agli aspiranti docenti. Pubblichiamo di seguito le soluzioni.
Le prove STEM per docenti – soluzioni
1. Sia assegnato un triangolo rettangolo di vertici A, B, C e angolo retto in A, avente perimetro di 12 cm. Nel triangolo è inscritto un cerchio di raggio uguale a 1 cm. Indicato con R il punto di tangenza tra il cerchio e il lato AB, si verifica che il segmento RB misura 3 cm. Indicato con K il punto di tangenza tra il cerchio e il lato BC, la lunghezza del segmento CK è: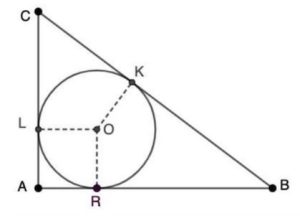
a. 2 cm b. 3 cm c. 4 cm d. (3/2) cm
1. SOLUZIONE. I segmenti di tangenza sono a due a due congruenti, per cui KB = RB = 3 cm e AR = AL = 1 cm. A questo punto possiamo calcolare CK = [12 – (3•2) – (1•2)] / 2 = 2 cm. Risposta a.
2. Cecilia possiede due dadi indistinguibili con le facce numerate da 1 a 6. Uno dei due dadi è regolare, mentre l’altro è truccato; nel dado truccato, la probabilità che esca valore 1 è pari a 3/8 mentre le rimanenti facce hanno ciascuna probabilità 1/8. Qual è la probabilità che, lanciando uno dei due dadi a caso, si ottenga il valore 3?
a.15/96 b. 5/36 c. 7/48 d. 1/8
2. SOLUZIONE. Ciascun dado può essere scelto con una probabilità pari a 1/2. Nel dado non truccato la probabilità di uscita del 3 è pari a 1/6, mentre nel dado truccato è pari a 1/8, per cui la probabilità cercata è pari a 1/2 • 1/6 + 1/2 • 1/8 = 1/12 + 1/16 = 7/48. Risposta c.
3. In un triangolo di vertici A, B e C, il lato AB misura 4 m. il lato BC 6 m. il lato CA 5. Sul lato BC si considera il punto O che dista 1 m da B. Siano A’, B’, C’ i vertici del triangolo simmetrico di ABC rispetto a O (simmetria centrale). Il perimetro del poligono non convesso ABC’A’B’C formato dal triangolo e dal suo simmetrico misura: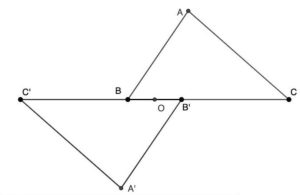
a. 30 m. b. 26 m. c. 24 m. d. 28 m.
3. SOLUZIONE. Sappiamo che BC misura 6 m e OB = OB’ misura 1 m per cui BC’ = B’C misurerà 4 m. Ora sommiamo i lati 4 + 5 + 4 + 4 + 5 + 4 = 26 m. Risposta b.
4. Alle ultime elezioni comunali lo schieramento A ha preso il 60% dei voti mentre lo schieramento B ne ha presi il 40%. Si sa che il 50% di coloro che hanno votato lo schieramento A è favorevole all’apertura del centro storico alle auto, mentre solo il 30% di coloro che hanno votato lo schieramento B è favorevole all’apertura del centro storico alle auto. Se un elettore scelto a caso è favorevole all’apertura del centro storico alle auto, qual è la probabilità che abbia votato lo schieramento B?
a. 6/19 b. 2/7 c. 9/19 d. 3/5
4. SOLUZIONE. Consideriamo 100 elettori di cui 60 hanno votato A e 40 B. I favorevoli all’apertura sono 30 elettori A e 12 elettori B per un totale 42 elettori. Ora 12 sono i favorevoli all’apertura del centro storico che hanno votato B sul totale di 42 dei favorevoli, quindi 12 / 42 che semplificato diviene 2/7. Risposta b. Si può applicare la formula generale di Bayes, P(B|fav) = P(fav|B)•P(B) / P(fav|B)•P(B) + P(fav|A)•P(A), da cui la probabilità cercata è pari a P(B|fav) = (0,3 • 0,4) / (0,3 • 0,4 + 0,5 • 0,6) = 0,12 / (0,12 + 0,3) = 0,12 / 0,42 = 2/7.
5. Il raggio della circonferenza G circoscritta a un triangolo ABC è pari a 5 cm e il lato AB è lungo 6 cm. Sapendo che il punto A’, simmetrico di A rispetto al segmento BC, appartiene alla circonferenza G, l’area del quadrilatero ABA’C è pari a: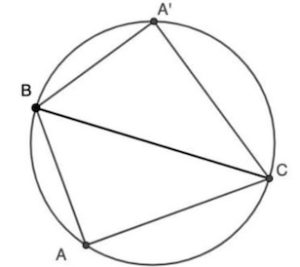
a. 48 cm2 b. 30 cm2 c. 24 cm2 d. 36 cm2
5. SOLUZIONE. Per simmetria BC è il diametro del cerchio e quindi misura 10 cm. Sappiamo che AB misura 6 cm ed è il cateto del triangolo rettangolo ABC. Ora con Pitagora troviamo AC = √ (102 – 62) = 8 cm. Infine il triangolo ABC ha area 6 • 8/2 = 24 cm2 e il quadrilatero 48 cm2. Risposta a.
6. Sei ragazzi europei, due americani e tre africani sono gli 11 giocatori di una squadra di calcio. Sono sorteggiati a caso due di essi. Qual è la probabilità che sia sorteggiato almeno un africano?
a. 18/55 b. 11/55 c. 5/11 d. 27/55
6. SOLUZIONE. La probabilità che non venga sorteggiato alcun africano è pari a 8/11 ⋅ 7/10 = 28/55, da cui la probabilità cercata è pari a 1 − 28/55 = 27/55. Risposta d.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Bellissimi esercizi del lunedì. Fatti facilmente 4 su 6, quindi geometria sto migliorando. Ma ho gravi lacune in calcolo delle probabilità. Mi ci metto appena finito il ripasso di trigonometria. Il bello è che quasi 30 anni fa mi ero laureata in statistica 😱😱😱, ma ero una ragazza davvero inconsapevole….. oggi tutta un’altra faccenda 😅😅😅