73. Soluzioni del 12 dicembre 2022 – Un Calendario dell’Avvento per matematici

Le soluzioni del 12 dicembre 2022 a cura di Fabio Ciuffoli

Ieri abbiamo proposto tre giochi tratti dallo speciale Calendario dell’Avvento pubblicato dal sito Mathigon – Parco Giochi della Matematica e di seguito presentiamo le soluzioni. 

Un Calendario dell’Avvento per matematici – soluzioni 

1. Un triangolo isoscele è posto all’interno di un quadrato. Il cerchio celeste è inscritto nel triangolo isoscele e il cerchio blu è inscritto in uno dei due triangoli rettangoli disegnati su entrambi i lati. Qual è il rapporto tra il raggio del cerchio celeste e il raggio del cerchio blu?

1. SOLUZIONE. Ci sono diversi metodi per arrivare alla soluzione, ad esempio con la trigonometria, tuttavia una delle soluzioni più eleganti utilizza questa formula per l’area di un triangolo:  

Area triangolo = 1/2 (perimetro * r del cerchio inscritto).

[L’area di un triangolo è la metà del suo perimetro moltiplicato per il raggio del suo cerchio inscritto.]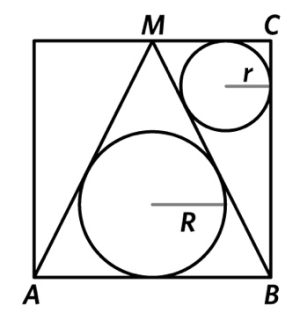Supponiamo che il quadrato abbia il lato di lunghezza 2 e indichiamo con R il raggio del cerchio maggiore e con r il raggio di quello minore. Con Pitagora, possiamo calcolare la lunghezza dei due cateti del triangolo isoscele

AM = MB = √(2² + 1²) = √5

Per simmetria, l’area del triangolo isoscele AMB è il doppio dell’area del triangolo più piccolo BCM, quindi Area AMB = 2(Area BCM). Applicando la formula otteniamo:

1/2 (2 + √5 + √5) • R = 2 • 1/2 (1 + 2 + √5) • r    da cui (1 + √5) • R = (3 + √5) • r

e infine  R/r = (3 + √5) / (1 + √5)    da cui (1 + √5) / 2 = φ.

Interessante, questo è il numero del rapporto aureo collegato generalmente a bellezza e armonia!

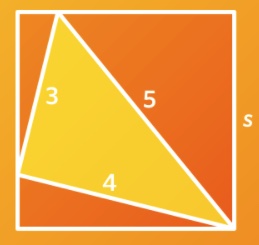
2. Il triangolo di lati 3, 4 e 5 si trova all’interno di un quadrato. Qual è l’area del quadrato?

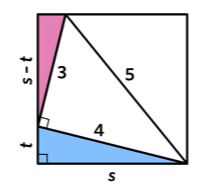2. SOLUZIONE. È noto che un triangolo di lati 3, 4 e 5 è rettangolo. Osservando la figura, in base alle proprietà degli angoli supplementari, possiamo vedere che i triangoli rosso e blu hanno gli stessi 3 angoli interni e quindi sono simili.Perciò (s − t) / 3 = s / 4 da cui t = s/4. Ora con Pitagora: s² + t² = 4² poi sostituendo: s² + (s/4)² = 16 che diviene (17/16) s² = 16  e infine l’area del quadrato s²= 256/17 ≈ 15.

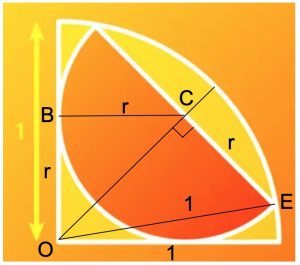Con Pitagora calcoliamo l’ipotenusa OC = √ (r² + r²) che diviene OC = r√2. Ora applicando Pitagora al triangolo OCE, che ha l’ipotenusa pari a 1 poiché questa è il raggio del cerchio grande, avremo (r√2)² + r² = 1²  che diviene 3r² = 1, quindi  r = √(1/3). Infine l’area del semicerchio arancione è π [√(1/3)]² /2 = π/(3 • 2) = π/6.