
I Giochi del Lunedì di Prisma del 12 dicembre 2022 a cura di Fabio Ciuffoli
Il sito web Mathigon – Parco Giochi della Matematica – propone ogni anno uno speciale Calendario dell’Avvento, pubblicando un problema al giorno dall’1 al 24 dicembre. Anche quest’anno abbiamo selezionati tre giochi e invitiamo i lettori a presentarci le loro osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Alle ore 17.00 di domani pubblicheremo le soluzioni.
Un Calendario dell’Avvento per matematici
1. Un triangolo isoscele è posto all’interno di un quadrato. Il cerchio celeste è inscritto nel triangolo isoscele e il cerchio blu è inscritto in uno dei due triangoli rettangoli disegnati su entrambi i lati. Qual è il rapporto tra il raggio del cerchio celeste e il raggio del cerchio blu?

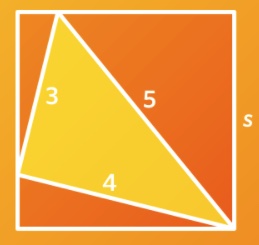
2. Il triangolo di lati 3, 4 e 5 si trova all’interno di un quadrato. Qual è l’area del quadrato?

I giochi sono tratti da Mathigon, il Parco Giochi Matematico, un bellissimo sito gratuito dove si trovano ottime animazioni interattive e altre iniziative per studenti, insegnanti e appassionati di matematica.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
11 risposte
La mia soluzione
Problema n° 3. ⇒raggio “r”(semicerchio)=1/√3,…. quindi abbiamo che l’area cercata è ⇒Area(semic. arancio)=π•1/6.
Vedi immagine
N. 2.
x =(12/17)*RADQ(17)
y = (3/17)*RADQ(17)
lato = (16/17)*RADQ(17)
Area del quadrato = 256/17 circa 15,05882353
Ho avuto un po di tempo e l’ho trascritto in bella.😀😀😀😀
Problema 1. Area semicerchio arancione = (Pigreco/6).
Ho intuito che i punti di tangenza disegnano un quadrato, insieme al centro del quadrante giallo e al centro del semicerchio arancione. Forse l’intuizione è sbagliata. Ora la verifico meglio e vedo di postare un disegno.
Mi riferivo al Problema 3, scusate.
Il raggio minore r risulta uguale a (1/radq3), per cui l’area arancione è uguale a (Pigreco/6).
Spero che l’intuizione sia giusta, perché così la soluzione mi pare molto elegante. 🙂
Perfetto, a domani per le soluzioni
N. 1. Perimetro triangolo isoscele: Lradq5+L. Perimetro triangolo rettangolo ((radq5)/2+3/2)L dove L è il lato del quadrato. Indicando con R1 e R2 i raggi si ottiene (Lradq5+L)R1=L^2 e ((radq5)/2+3/2)LR2=L^2/2. Da cui si ottiene: R1/R2=(radq5+3)/(radq5+1)
Problema n°2 ⇒il lato del quadrato viene ⇒ s=16/√17 e quindi l’area dello stesso è ⇒ s²=256/17. Vedi allegato grafico.
Problema 2: 256/17.
Soluzione al problema 1 vedi immagine.