127. Soluzioni del 15 luglio 2024 – L’istinto matematico
Nessun commento
Menu
I Giochi del Lunedì di Prisma del 13 giugno 2022 a cura di Fabio Ciuffoli
Oggi presentiamo due problemi proposti dal professor Valerio Pattaro, che rimandano alla geometria proiettiva e alla teoria dei frattali. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione nello spazio riservato ai comenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
La colonna blu e i cerchi nel triangolo
1. Determinare l’altezza della colonna blu, sapendo che la colonna rossa è alta 2 metri e proietta un’ombra lunga 3 metri, mentre l’ombra della colonna blu è spezzata in due parti, una prima parte di 6 metri sul pavimento e una seconda parte di 4 metri sul muro ortogonale rispetto al pavimento. Si suppone che i raggi luminosi siano paralleli.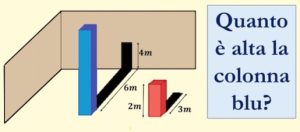
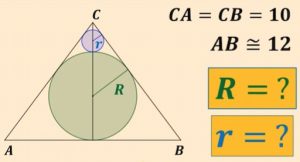
2. Il triangolo ABC è isoscele con la base AB ≈ 12 e i lati obliqui CA = CB = 10. La circonferenza inscritta in verde ha raggio R, mentre una seconda circonferenza in blu, di raggio r, è tangente sia alla prima circonferenza che ai due lati del triangolo. Determinare i due raggi R e r.
Aggiornamento per le soluzioni click qui
I problemi sono tratti dal canale YouTube del professor Valerio Pattaro, insegnante di Matematica e Fisica nelle scuole superiori. Il canale è molto frequentato e si trovano ottime lezioni, molto chiare e interessanti. Una vera risorsa per studenti e insegnanti. https://www.youtube.com/c/ValerioPattaro
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
6 Responses
La soluzione al problema 1.
Problema n 2.
Quesito 2:
Se O è il centro della circonferenza di raggio R e T il punto di tangenza al lato BC, il triangolo TOC è simile al triangolo HAC, perciò TC = 4/3 R. Poiché CH = 8, CO = 8-R. Per il teorema di Pitagora R² + (4/3 R)² = (8-R)² da cui si ricava R=3 (la soluzione negativa non può essere accettata in quanto misura di un segmento). Analogamente si ricava che r=3/4.
CH è l’altezza del triangolo che può essere ricavata anch’essa attraverso il teorema di Pitagora: CH² = AC² – AH² cioè CH² = 10² – 6² da cui CH = 8.
Ottimo a domani per le soluzioni
Gioco 1. L’ombra del rettangolo rosso è 1,5 volte la sua lunghezza. Ora, considerando che l’ombra verticale del rettangolo blu è alta 4 metri, se non ci fosse stato il muro, la sua lunghezza a terra sarebbe stata 1,5 volte 4 quindi 6 mt i quali, sommati ai 6 mt a terra, fa un totale di 12 mt. Essendo l’ombra 1,5 volte il rettangolo, se ne deduce che il rettangolo blu è alto 8 mt.