
Le soluzioni del 13 giugno 2022 a cura di Fabio Ciuffoli
Ieri abbiamo presentato due problemi proposti dal professore Valerio Pattaro e di seguito pubblichiamo le soluzioni.
La colonna blu e i cerchi nel triangolo – soluzioni
1. Determinare l’altezza della colonna blu, sapendo che la colonna rossa è alta 2 metri e proietta un’ombra lunga 3 metri, mentre l’ombra della colonna blu è spezzata in due parti, una prima parte di 6 metri sul pavimento e una seconda parte di 4 metri sul muro ortogonale rispetto al pavimento. Si suppone che i raggi luminosi siano paralleli.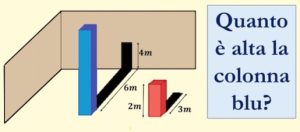
1. SOLUZIONE. Definiamo con x l’altezza della colonna blu e immaginando che la parete non ci sia, definiamo con a il prolungamento della sua ombra sul pavimento. In altri termini, la lunghezza a potrebbe essere l’ombra di un oggetto alto 4 metri. Ora i due triangoli rettangoli, rispettivamente con cateti 2 e 3 e con cateti 4 e a, sono simili, per cui 2 : 3 = 4 : a da cui a = 6. Anche il triangolo rettangolo con cateti x e (6 + a) è simile al triangolo rettangolo con cateti 2 e 3, per cui avremo 2 : 3 = x : (6 + a) da cui x = 24/3 = 8 m.
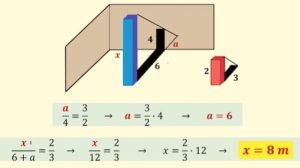
2. Il triangolo ABC è isoscele con la base AB ≈ 12 e i lati obliqui CA = CB = 10. La circonferenza inscritta in verde ha raggio R, mentre una seconda circonferenza in blu, di raggio r, è tangente sia alla prima circonferenza che ai due lati del triangolo. Determinare i due raggi R e r.
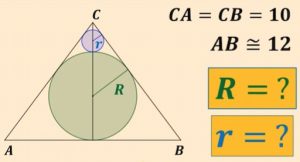
2. SOLUZIONE. Con riferimento al disegno sotto, calcoliamo HB che è metà della base = 6. Sappiamo che i segmenti di tangenza, uscenti dallo stesso punto, son congruenti, perciò BD = BH = 6 quindi CD = 10 – 6 = 4. Il triangolo CHB è rettangolo e con Pitagora determiniamo CH = √ 100 – 36 = 8. Ora i triangoli CHB e CDO sono simili perché: hanno un angolo in comune in C, entrambi sono triangolo rettangoli con angolo retto rispettivamente in H e in D e di conseguenza anche il terzo angolo sarà congruente. Possiamo quindi impostare la proporzione 8 : 6 = 4 : R e svolgendo R = 3. 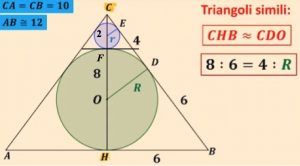
Ora determiniamo r. Calcoliamo CF = 8 – 6 = 2. Notiamo che il triangolino in alto, di altezza CF, ha la stessa struttura del triangolo ABC infatti è la stessa immagine rimpicciolita: Si tratta di una struttura frattale che si ripete uguale a se stessa sempre più piccola, quindi se l’altezza del triangolino è 2 e l’altezza del triangolo ABC è 8, tutti gli elementi dei triangoli saranno in proporzione 1 a 4. In questo modo, se il raggio R della circonferenza inscritta nel triangolo grande è 3, il raggio r della circonferenza inscritta nel triangolo piccolo sarà ¾. E si potrebbe proseguire così all’infinito, se costruissimo una circonferenza più piccola in alto, il suo raggio sarebbe 3/16 e poi ancora 3/62 e via di seguito.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Riporto di seguito il confronto tra Janpieter e Francesco, che trovo particolarmente interessante e costruttivo e li ringrazio per la partecipazione.
Janpieter van Dijk: Forse bisogna spiegarlo così ai ragazzi a scuola:
(1) Il rapporto altezza – ombre rimane uguale per tutti casi (si chiama tangente dell’angolo: altezza/lunghezza sarebbe sin/cos).
(2) Quel rapporto è dunque 2/3 (dedotto della colonna rossa).
(3) Il pezzo da 4 metri in verticale dell’ombra del blu lascierebbe un’ombra aggiuntiva di 6 metri (usi il rapporto 2/3).
(4) Dunque l’ombra totale della colonna blue diventa 12 metri.
(5) Con un ombra da 12 metri la colonna blu è alta 8 metri (usi il rapporto 2/3).
Francesco Conserva a Janpieter van Dijk: Così è inutilmente contorto e complicato.
L’ombra sul muro (parallelo alla colonna) è già in vera forma e grandezza, non occorre trasformarla in ombra virtuale orizzontale, fare calcoli e ritornare a 4, perché il 4 ce lo hai già.
Quindi, giusto applicare il rapporto alle ombre oriźzontali e poi, semplicemente, sommare l’altezza sul muro.
Janpieter van Dijk a Francesco Conserva: ho capito quello che vuoi dire. In senso che l’ombre da 6 metri rappresenta una colonna da 6*2/3=4, e poi la punto sopra che non ha fatto ombra sono 4 m. Dunque 4+4. Io sto solamente provando di spiegare a persone come allievi in una scuola la logica dietro il calcolo. E visto che ogni persona mentalmente è fatto in modo diversa, talvolta una spiegazione in un modo o in un’altra funziona meglio. Dunque non è che sono in disaccordo con te ma per me nessuna spiegazione è “inutile e contorta”. Diciamo che “inutile” non lo è perché per alcune persone potrebbe funzionare meglio che l’altra, e “contorto” non è perché non ha nessun problema di logica. Potremmo anche convertire tutto con acos e asin, o calcolare le lunghezze delle ipotenuse, se vogliamo quantizzare tutto, o convertirlo in un algoritmo per codificare. Talvolta una generalizzazione diventa più lungha ma non “contorta”. Ciao e buona giornata!
Janpieter van Dijk: Quindi in alternativa:
(1) Il rapporto altezza – ombre rimane uguale per tutti casi (si chiama tangente dell’angolo: altezza/lunghezza sarebbe sin/cos).
(2) Quel rapporto è dunque 2/3 (dedotto della colonna rossa).
(3) Applicando quel rapporto l’ombre di 6 m della colonna blu rappresenta dunque una altezza di 4 m per la parte inferiore della colonna blu.
(3) Il pezzo da 4 metri in verticale dell’ombra del blu è l’ombra della parte superiore della colonna blu.
(4) Dunque l’altezza totale della colonna blue diventa 4+4=8 metri.
Francesco Conserva a Janpieter van Dijk: Il mio “inutilmente contorto e complicato” era riferito alla considerazione che, quando si possono evitare calcoli è opportuno evitarli, vuoi per ridurre le possibilità di errore, vuoi per la perdita di precisione indotta da eventuali approssimazioni dei decimali.
Invece, è apprezzabile il tuo ragionamento dal punto di vista didattico, perché stimulate riflessioni ragionamenti ed abitua ad approcciarsi da punti di vista diversi.
Janpieter van Dijk: Perfettamente d’accordo con te!🙂🙂 E aprezzo molto il tuo commento Francesco perché mi associo con le varie possibilità di approcciare i problemi che tu giustamente hai descritto: Ho notato che alcuni ragazzi/persone, quando spieghi in un modo più lungho arrivano a comprendere. E dall’altro lato, il lato opposto, per esempio in algoritmi di calcolo l’arte è proprio di abbreviare al massimo per velocizzare i calcoli, anche usando formulazioni che in se stessi sono derivati da accumuli di relazioni e da soli a prima vista non rivelano il loro senso. 👍👍