
I Giochi del Lunedì di Prisma del 30 maggio 2022 – La geometria di Estrella
Oggi presentiamo quattro giochi matematici proposti da Estrella Fernández, insegnante di matematica e divulgatrice. Sul suo canale youtube si trovano ottime videolezioni spiegate in modo semplice e chiaro. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione nello spazio riservato ai commenti. Domani alla 17.00 pubblicheremo le soluzioni.
La geometria di Estrella
1. Calcolare la somma delle aree dei quadrati.
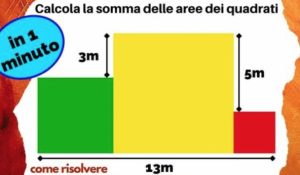
2. Determinare l’area colorata.
3. Calcolare l’area del rettangolo bianco.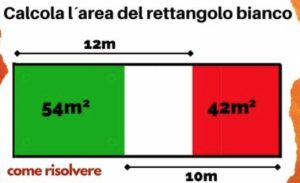
4. Calcolare l’area del quadrato che contiene cinque rettangoli colorati equivalenti.

Aggiornamento per le soluzioni click qui
I problemi sono tratti dal canale you tube di Estrella Fernàndez che ringraziamo per la disponibilità.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
20 risposte
1) 69 mq
2) Se unisco il punto A al centro e al punto medio della corda ottengo un triangolo rettangolo…col teorema di Pitagora ottengo i due raggi e calcolando la differenza ottengo 9 pi greco mq
3) 10 × 6 =60mq -42mq = 18 mq
4) A occhio 400 mq
Perfetto. Nel pomeriggio le soluzioni.
Problema 3. Se nel testo fosse esplicitato che si ricerca un valore intero per l’altezza comune e la larghezza del rettangolo bianco, si potrebbe procedere con un’euristica con cui si eviterebbe l’uso della messa in equazione… Valori accettabili per la larghezza sono 0, 1, 2, 3, 4, 5, 6, fino a 10… Per ogni valore si deduce il valore dell’altezza dei due rettangoli che deve essere comune… eccetera
Problema 4. Sia c il cateto del quadrato diviso in 5 zone di aree uguale. Il rettangolo viola misura c×c/5, di area c²/25. Il rettangolo azzurro misura 5×(c-c/5), cioè 5×4c/5, su area e pari a 4c; essendo che 4c=c²/5, ottenemo 4=c/5, cioè c=20. Allora l’area del quadrato grande vale 400m², l’area viola 20m×4m, l’area azzurra 16m×5m, la verde 15m×5,333…m, le aree rossa e gialla 7,5m×10,666…m.
Sia x la base del rettangolo bianco, abbiamo 54/(12-x)=42/(10-x), da cui
54(10-x)=42(12-x), quindi
540-54x=504-42x, e
36=12x, x=3m.
Da cui l’altezza degli rettangoli è pari a 54/(12-3), ovvero 6m.
Finalmente troviamo l’area in del rettangolo bianco, cioè 18m²
Perfetto. Nel pomeriggio le soluzioni.
1) Se indico con A, B e C i lati dei 3 quadrati, B=A-3, C=A-5, A+B+C013 -> A=7, B=4, C=2, A^2+B^2+C^2=69 m^2;
3) 54/(12-x)=42/(10-x), x base del rettangolo bianco, -> x=3m, altezza rettangolo bianco = 6m, Area=18 m^2;
4) b= base rettangolo blu, a= base rettangolo rosso, h= altezza rettangolo rosso,
sistema 1) (b-a) 2h = ah, 2) ah=5b, 3) (5+2h-b)(5+2h)=ah, da cui h=15/2, b=16, a=32/3, per cui Area =400 m^2
2) R = raggio circonferenza maggiore, r =raggio ciconferenza minore, applicando Pitagora R^2-r^2=9, quindi area colorata = Pi(R^2-r^2)= 9 Pi m^2, Pi = pi greco
Perfetto a domani per le soluzioni
Perfetto a più tardi per le soluzioni.
Problema 1. Sia g il lato del quadrato giallo, v quello del verde e r quello del rosso. Abbiamo (g-3)+g+(g-5)=13, cioè 3g-8=13, da cui 3g=21 e g=7. Allora v=g-3=4 e r=g-5=2.
La somma delle aree in m² e quindi
4²+7²+2²=69
Problema 1. a+b+c=13 ; b-a=3 ; b-c=5 ; a=7 ; b=4 ; c=2 ; Area_tot=69m^2
Problema 1. Per trovare l’area del quadrato più grande: x+x-3+x-5= 13
3x= 13+5+3
3x=21
x=7
Quindi il lato del quadrato verde è 7-3=4
Il lato del quadrato rosso è 7-5=2
Sommando le aree viene
7*7+4*4+2*2=69
Problema 1
Lato quadrato giallo = x
Lato quadrato verde = x – 3
Lato quadrato rosso = x – 5
(x – 3) + x + (x – 5 ) = 13
3x = 21 x = 7 area = 49 quadrato giallo
lato = 4 area = 16 quadrato verde
lato = 2 area = 4 quadrato rosso
Area dei 3 quadrati = 69
Perfetto, a domani per le altre soluzioni.
Supponiamo lato rosso =1 allora lato giallo sarebbe 6 e quindi lato verde =6 —-IMPOSSIBILE.
Supponiamo lato rosso =2 allora lato giallo sarebbe 7 e lato verde = 4 POSSIBILE
Supponiamo lato rosso = 3 allora lato giallo sarebbe 8 e quindi lato verde =3 —-IMPOSSIBILE.
SOLUZIONE 4×4+7×7+2×2 = 69
Perfetto a domani per le altre soluzioni
Problema 3.
12x-54=10x-42
2x=12
x=6
base verde=54/6=9
base rossa=42/6=7
base bianca=12-9=10-7=3
area bianca=3×6=18m^2
Sia O il centro degli due cerchi e T il punto di tangenza della corda al cerchio minore. Allora il triangolo AOT e rettangolo isoscele e il raggio OT e pari a 3cm, il raggio OA a 3√2cm, l’area del cerchio maggiore vale 18πcm² e quella del cerchio minore 9πcm², da cui l’area gialla e pari a 9πcm².
Area gialla=9*(pi greco) poiché detti y e x rispettivamente il raggio maggiore e quello minore l’area gialla è pi*(y^2-x^2) ma (y^2-x^2)=9 per il teorema di Pitagora.
Risposta al problema 2
Tracciamo il raggio esterno R in un estremo della corda e quello interno r nel punto di tangenza. Dal teorema di Pitagora R^2-r^2=9
L’area richiesta è data da πR^2-πr^2=9π