Menu
Le soluzioni del 30 maggio 2022 a cura di Fabio Ciuffoli
Ieri mattina abbiamo presentato quattro giochi proposti da Estrella Fernandez e ora pubblichiamo le soluzioni.
La geometria di Estrella – soluzioni
1. Calcolare la somma delle aree dei quadrati.
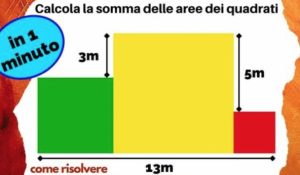
1. SOLUZIONE. Definiamo x il lato del quadrato rosso e avremo: x + (x + 5) + (x + 5 – 3) = 13 da cui 3x = 6 quindi x = 2. Area quadrato rosso: 22 = 4 mq. Area quadrato giallo: (5 + 2)2 = 49 mq. Area quadrato verde: (13 – 7 – 2)2 = 16 mq. Area dei quadrati = 4 + 49 + 16 = 69 mq.
2. Determinare l’area colorata.
2. SOLUZIONE. Definiamo O il centro dei due cerchi e tracciamo il triangolo rettangolo che ha per ipotenusa il raggio OB e per cateti il raggio del cerchio più piccolo e metà corda AB. Chiamando R e r rispettivamente i raggi del cerchio grande e del cerchio piccolo, avremo: R2 = 9 + r2. L’area colorata è data dalla differenza tra l’area del cerchio grande e l’area del cerchio piccolo: πR2 – πr2 = π(9 + r2) – πr2 = π9 ≈ 28,26 mq.
3. Calcolare l’area del rettangolo bianco.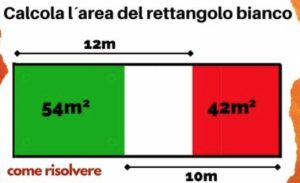
3. SOLUZIONE. Definiamo h l’altezza dei rettangoli e avremo: 10h – 42 = 12h – 54 da cui 2h = 12 quindi h = 6m. La base del rettangolo verde è 54/6 = 9m e la base del rettangolo rosso è 42/6 = 7m. Per differenza calcoliamo la base del rettangolo bianco 10 – 7 = 3m. Infine, l’area del rettangolo bianco è 3 * 6 = 18 mq.
4. Calcolare l’area del quadrato che contiene cinque rettangoli colorati equivalenti.
4. SOLUZIONE. Definiamo A l’area di un rettangolo, avremo: base blu = A/5. Altezza verde (considerando i tre rettangoli verde, giallo e rosso) 3A / (A/5) = 15 m. A questo punto possiamo determinare il lato del quadrato che è 15 + 5 = 20 m. L’area del quadrato è 400 mq.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
2 risposte
Un altro modo:
Lato quadrato= L
Lato corto del rettangolo viola: c
Lato lungo rettangolo blu: b
Area viola: L•c=(1/5)L^2 segue: c=(1/5) L
b=L-c= (4/5) L
Area blu=(1/5) L^2
(5m•b) =(1/5) L^2 ma b=(4/5) L quindi 4L=(1/5) L^2 da cui 20L=L^2 quindi L=20 e L^2=400.
Segnalo la soluzione del problema 2 proposta da Emanuele Zeppieri che ha scritto: “Metodo più semplice di tutti: visto che il problema ha 1 grado di libertà, mi metto nella situazione (estrema) in cui il punto di tangenza col cerchio interno (bianco) coincide col centro dei due cerchi e, di conseguenza, l’area gialla coincide con l’intera area del cerchio esterno. In queste condizioni la corda AB è un diametro del cerchio esterno, la cui area vale pertanto: 3²π = 9π m²”.
Ottimo il metodo della estremizzazione. Grazie per la partecipazione.