121. Soluzioni del 22 aprile 2024 – Cerchi e triangoli sangaku
Nessun commento
Menu
I Giochi del Lunedì di Prisma del 2 maggio 2022 a cura di Fabio Ciuffoli
Oggi proponiamo tre problemi sul rotismo ovvero sui sistemi di ruote e piani collegati tra loro in modo da consentire la trasmissione del moto. Iniziamo con un gioco abbastanza noto e relativamente semplice, poi procediamo con altri due problemi più complessi e apparentemente controintuitivi. Invitiamo i lettori a presentarci osservazioni e proposte di soluzione nello spazio riservato ai commenti. Alle ore 17.00 di domani pubblicheremo le soluzioni e le relative dimostrazioni.
Rotismi
1. Prendete due monete da un euro e disponetele su un tavolo, come in figura. Ora spostate la moneta in alto, facendola rotolare lungo mezza circonferenza della moneta sottostante. In quale posizione, A, B, C o D, verrà a trovarsi la moneta spostata, quando sarà esattamente sotto la moneta intorno alla quale ha ruotato?
2. I due cerchi, B e B1, sono fissi e sono uguali di raggio 3. I due cerchi, A e A1, sono mobili e sono uguali di raggio 1, il cerchio A è esterno al cerchio B, mentre il cerchio A1 è interno al cerchio B. Quante rotazioni su se stessi compiono A e A1 per completare un giro rispettivamente all’esterno di B e all’interno di B1?
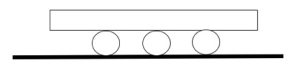
3. Un grosso blocco di marmo viene trascinato su tre tronchi, come disegnato in figura. I tronchi hanno tutti un ugual diametro di 50 cm. Qual è la distanza percorsa dal masso ogni volta che i tronchi compiono una rotazione?
Aggiornamento per le soluzioni click qui
I problemi 1 e 3 sono stati trattati nei libri di sui sono autore: “Giochi, esercizi e test di creatività” e “Giochi matematici e logici”. Il problema 2 è un classico problema di rotismo epicicloidale facilmente reperibile in rete.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
14 risposte
Problema n. 3. Vi è um avanzamento della ruota pari a 50*PI e altrettanto avanzamento del punto rispetto alla ruota ovvero in totale lo spostamento è pari al doppio della distanza percorsa dal punto ovvero 2*50*pi
Perfetto
1 C
3 50 pi greco
Bene il primo. Oggi pomeriggi le soluzioni con dimostrazione.
Sul problema 3. Se i tronchi fossero fissati rotando su un asse, la massa si sposterebbe π×50, cioè circa 157cm.
Ma siccome i tronchi rotolano sulla terra, il loro centro si sposta anche di 157cm.
Da cui, la massa si sposta di circa 314cm per ogni giro degli tronchi.
Carmelo Giugno, che ringrazio per la disponibilità, ha presentato su questo argomento un interessante problema che ripropongo di seguito:
Due circonferenze mobili, (1) di raggio r e (2) di raggio r – 10 mm, rotolano, senza strisciare, sulle superfici delle circonferenze fisse (1) di raggio R1 = 280 mm e (2) di raggio R2 = 270 mm. In figura 1 il rotolamento è all’ esterno della circonferenza fissa, mentre in figura 2 è allo interno della circonferenza fissa.
Quando i centri, m1 e m2, delle due circonferenze mobili compiono un giro completo intorno ai centri, f1 e f2, delle circonferenze fisse, entrambe le circonferenze mobili compiono lo stesso numero di giri, n, intorno ai propri centri.
Determinare r ed n.
La soluzione domani pomeriggio alle 17.00. Grazie Carmelo.
Buongiorno !!✅ Problema 1)⇒quando la moneta esterna ha fatto un giro si troverà nella posizione C), proprio come quando ne avrà fatti due e si troverà nella stessa identica posizione iniziale !!✅ Problema 2)⇒ nel 1°caso il rapporto di trasmissione→(A esterna) è (R+r)/r=4 giri, nel 2° caso il rapporto di trasmissione→(A₁ interna) è (R₁–r₁)/r₁=2 !!✅ Problema 3)⇒ la lastra di marmo avrà fatto Ⅼ=2∙π∙r=100∙π
Ottimo. A domani per le soluzioni e un nuovo problema, inverso, sul rotismo.
2.
Nella rotazione esterna, c’è una rivoluzione “positiva” quindi si guadagna 1 rotazione in più (vedi anche il problema 1: dopo mezzo giro, la moneta ha già fatto una rotazione completa). Quindi fa 4 giri.
Quando la moneta è interna, la rivoluzione è “negativoscopi” e perde un giro. Quindi fa 2 giri.
3.
Come sopra: il tronco fa una rivoluzione “positiva” rispetto al masso, quindi il masso avanza di 2 circonferenze complete (il tronco è avanzato di una circonferenza) cioè 100pigreco, circa 314
Interpretazione fisica:
Il punto del tronco a contatto con il masso, viaggia a velocità doppia, rispetto al centro del tronco in quanto il suo “raggio” é doppio, nella rotazione con centro nel punto di contatto tra tronco e piano. Perciò nello stesso tempo percorre distanza doppia (rispetto al centro che si è spostato di una sola circonferenza).
Perfetto. A domani per le soluzioni, dove prsenteremo un ulteriore problema.
Problema n. 2.
La questione controintuitiva la associo alla difficoltà di immaginare le caratteristiche di oggetti astratti, come i cerchi geometrici.
nello specifico l’assenza di spessore delle linee perimetrali.
è possibile tagliare il cerchio grande (r = 3) e distendere il suo perimetro formando un segmento di lunghezza 3×2×pigreco.
ipotizziamo che il segmento sia orizzontale.
i 2 cerchi piccoli (r = 1) saranno, in questo caso, uno sopra ed uno sotto il segmento prima generato.
possiamo tagliare anche questi due cerchi, per ottenere due segmenti, sopra e sotto, di lunghezza 1x2xpigreco.
la relazione che intercorre tra il segmento (perimetro) del cerchio grande e quello del cerchio piccolo è ora, con ogni possibile evidenza = 3.
che equivale al numero delle rotazioni delle due circonferenze piccole IDEALI attorno alla circonferenza grande IDEALE.
In questo modo non tieni conto del moto di rivoluzione dei cerchi piccoli (A e A1) rispetto ai cerchi grandi e fissi (B e B1) e quindi la risposta non è corretta. A domani per le soluzioni.
1. C
2. 4 in entrambi i casi
3. 50 * π = 157 cm circa
Buongiorno Giuseppe, bene la 1, ma le altre sue non sono così. A domani per le soluzioni.