
Le soluzioni del 2 maggio 2022 a cura di Fabio Ciuffoli
Ieri abbiano proposto tre problemi sul rotismo e ora presentiamo le soluzioni con dimostrazione.
Rotismi – soluzioni
1. Prendete due monete da un euro e disponetele su un tavolo, come in figura. Ora spostate la moneta in alto, facendola rotolare lungo mezza circonferenza della moneta sottostante. In quale posizione, A, B, C o D, verrà a trovarsi la moneta spostata, quando sarà esattamente sotto la moneta intorno alla quale ha ruotato?
1. SOLUZIONE. La moneta verrà a trovarsi nella posizione C. Sembra strano, molti si aspettano che la moneta, percorrendo una lunghezza pari a metà della sua circonferenza, venga a trovarsi capovolta. Questa aspettativa, intuitiva ma errata, non tiene conto del movimento di rivoluzione, della moneta spostata, intorno al centro della moneta che rimane ferma. Tecnicamente viene definito “rotismo epicicloidale esterno”.
2. I due cerchi, B e B1, sono fissi e sono uguali di raggio 3. I due cerchi, A e A1, sono mobili e sono uguali di raggio 1, il cerchio A è esterno al cerchio B, mentre il cerchio A1 è interno al cerchio B. Quante rotazioni su se stessi compiono A e A1 per completare un giro rispettivamente all’esterno di B e all’interno di B1?
 2. SOLUZIONE. Il cerchio A compie 4 rotazioni, il cerchio A1 ne compie 2. Il cerchio A gira su sé stesso (rotazione) e intorno al centro di B (rivoluzione) così compie un giro in più rispetto a 3 che è il rapporto tra le due circonferenze.
2. SOLUZIONE. Il cerchio A compie 4 rotazioni, il cerchio A1 ne compie 2. Il cerchio A gira su sé stesso (rotazione) e intorno al centro di B (rivoluzione) così compie un giro in più rispetto a 3 che è il rapporto tra le due circonferenze.
Nel caso del cerchio interno, il giro va sottratto perché rotazione e rivoluzione sono in senso opposto fra loro, quindi A1 tornerà nella posizione iniziale compiendo due rotazioni.
Molte persone sono tratte in inganno e rispondono “tre rotazioni”, pensando che entrambi i cerchi ruotino intorno al proprio centro, mentre in questo problema i cerchi B e B1 sono fissi e i cerchi A e A1 sono mobili, si tratta quindi di rotismo epicicloidale.
Osservazione interessante: se posizionassimo il cerchio piccolo con il suo piano ortogonale rispetto al piano del cerchio grande e procedessimo alla rotazione, allora il cerchio piccolo compirebbe 3 rotazioni, annullando l’effetto epicicloidale.
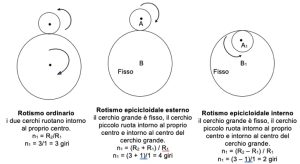
Per completezza, illustriamo tre casi di rotismo: ordinario, epicicloidale esterno e epicicloidale interno. Nelle formule sono indicati con n1 il numero di giri dei cerchi piccoli, con R1 il raggio dei cerchi piccoli e con R2 il raggio dei cerchi grandi.
Infine, riportiamo il testo di una domanda a risposta multipla del test attitudinale SAT del 1982, a cui furono sottoposti 300.000 studenti statunitensi, che fece scalpore per un clamoroso errore perché mancava la risposta corretta.
Il raggio del cerchio A è 1/3 del raggio del cerchio B, come disegnato in figura 4. Il cerchio A rotola intorno al cerchio B fino a tornare al punto iniziale. Quante rotazione compie A? 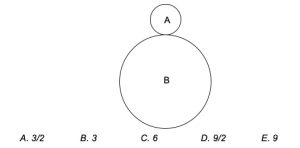
La risposta corretta, 4 rotazioni, non era compresa tra quelle predisposte dalla commissione esaminatrice. Le ripercussioni furono imbarazzanti e quando l’errore fu scoperto, se ne parlò sul “New York Times” e sul “Washington Post”. La risposta che gli esaminatori ritenevano corretta era la B ossia 3 rotazioni, non avevano tenuto del moto di rivoluzione!
3. Un grosso blocco di marmo viene trascinato su tre tronchi, come disegnato in figura. I tronchi hanno tutti un ugual diametro di 50 cm. Qual è la distanza percorsa dal masso ogni volta che i tronchi compiono una rotazione?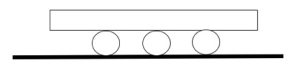
3. SOLUZIONE. La distanza percorsa è 3,14 metri e più in generale è il doppio della circonferenza dei tronchi. La pietra si muove in rapporto ai tronchi ed i tronchi in rapporto al terreno, per cui il blocco di marmo percorre due volte la circonferenza: 0,5 * 3,14 * 2 = 3,14. Questa soluzione sembra controintuitiva! Invitiamo il lettore a svolgere l’esperimento, utilizzando lattine di bibita o qualcosa di simile al posto dei tronchi ed un libro o un assetta di legno al posto del blocco di marmo e prendere le relative misure con un righello. Diverso sarebbe il caso in cui ci fosse un perno al centro di ogni ruota, ad esempio se il trasporto fosse effettuato mediante un carro, in questo caso la distanza percorsa dal blocco, dopo una rotazione dei tronchi, sarebbe esattamente uguale alla circonferenza di un tronco.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Ripropongo in questo spazio dei commenti per le soluzioni, il problema inverso posto da Carmelo Giugno e la relativa soluzione e disegno esplicativo. Grazie a Carmelo per l’ottimo lavoro.
Due circonferenze mobili, (1) di raggio r e (2) di raggio r – 10 mm, rotolano, senza strisciare, sulle superfici delle circonferenze fisse (1) di raggio R1 = 280 mm e (2) di raggio R2 = 270 mm. In figura 1 il rotolamento è all’ esterno della circonferenza fissa, mentre in figura 2 è allo interno della circonferenza fissa.
Quando i centri, m1 e m2, delle due circonferenze mobili compiono un giro completo intorno ai centri, f1 e f2, delle circonferenze fisse, entrambe le circonferenze mobili compiono lo stesso numero di giri, n, intorno ai propri centri.
Determinare r ed n.
SOLUZIONE. Si tratta di un problema di rotismo epicicloidale interno e esterno. In base alle regole, illustrate in precedenza, possiamo impostare la seguente uguaglianza:
(280 + r) / r = [270 – (r – 10)] / (r – 10);
che diviene (280 + r) (r – 10) = r (280 – r);
poi 280r – 2.800 + r2 – 10r = 280r – r2; r2 – 10r – 2.800 = 0
svolgendo l’equazione di secondo grado: r = 40.
Infine n = (280 + 40) / 40 = 8.
vedi figura allegata