33. Soluzioni del 28 febbraio 2022 – Olimpiadi di Matematica Junior in UK

Le soluzioni del 28 febbraio 2022 a cura di Fabio Ciuffoli

Ieri mattina abbiamo proposto tre giochi matematici tratti dalle prove Junior Mathematical Olympiad,  per i ragazzi della scuola primaria, predisposte dallo United Kingdom Mathematics. Ora presentiamo le soluzioni con dimostrazione. 

Olimpiadi di Matematica Junior (JMO) – soluzioni 

1. In questa somma di parole, ogni lettera rappresenta una delle cifre 0–9. Nessun numero inizia con 0. A quale cifra corrisponde ciascuna lettera?

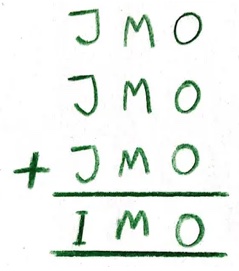
1. SOLUZIONE. Per determinare O, sommiamo tre volte O per trovare quel numero che ha una O al posto delle unità. Le uniche cifre che soddisfano questa condizione sono 0 e 5.

Se O = 0, non ci sono decine da “riportare” nella colonna centrale e quindi cerchiamo una cifra per M, per la quale tre M hanno una M al posto delle unità. Pertanto anche M è 0 o 5, ma se O = 0 allora avremo M = 5, poiché lettere diverse indicano cifre diverse.

 Se O = 5, il totale di tre O è 15 e quindi abbiamo un “1” da “riportare” nella colonna centrale. Tuttavia, non ci sono valori di cifre M, dove 3M + 1 fornisce M nella colonna delle unità. Quindi, O = 0 e M = 5. A questo punto: se J = 1, I = 4; se J = 2, I = 7; mentre se J > 2, ad esempio 3 o 4 ecc, non è possibile un numero del totale a 3 cifre. In conclusione ci sono solo due valori possibili per J. Le uniche soluzioni sono “JMO” = 150 con “IMO” = 450 e “JMO” = 250 con “IMO” = 750.

2. Nel diagramma seguente, un quarto di cerchio con raggio 3 cm è posizionato accanto a un quarto di cerchio con raggio 4 cm.

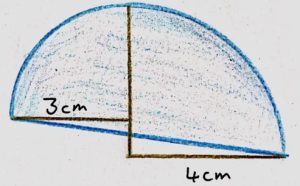
Qual è l’area ombreggiata totale delimitata dalle linee blu, in cm²?

2. SOLUZIONE. Estendiamo la linea di fondo per creare un rettangolo con altezza 1 cm e larghezza 3 cm.

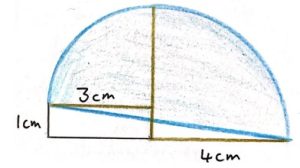
L’area di un cerchio è πr², quindi l’area delimitata dal perimetro della forma nel disegno sopra è l’area del rettangolo 3 x 1 più i due quarti di cerchio:

3 + (1/4)9π + (1/4)16π = 3 + (25/4)π

L’area ombreggiata, delimitata dalle linee blu, è data da questo valore meno l’area del triangolo di altezza 1 cm e base  (3 + 4) cm:

 3 + (25/4)π – 7/2. Infine, la risposta è (25/4)π – (1/2).

3. Un triangolo equilatero è diviso in triangoli equilateri più piccoli.

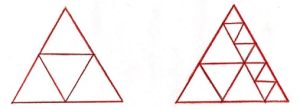
La figura a sinistra mostra che è possibile dividerlo in 4 triangoli equilateri. La figura a destra mostra che è possibile dividerlo in 13 triangoli equilateri. Quali sono i valori interi di n, dove n > 1, per i quali è possibile dividere il triangolo in n triangoli equilateri più piccoli?

3. SOLUZIONE. Chiamiamo triangolo originale il triangolo equilatero che deve essere diviso in triangoli equilateri più piccoli. Cominciamo con n = 2. C’è un modo per dividere il triangolo originale in due più piccoli? Non possiamo tracciare una linea da un vertice, poiché questo produrrebbe angoli inferiori a 60°. Ma se tracciamo una singola linea che disegna un triangolo equilatero, come in (a), creiamo un altro quadrilatero nel triangolo originale, non un triangolo. Quindi n non può essere 2.

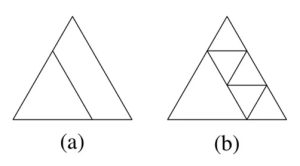
Se dovessimo dividere il quadrilatero in (a) in triangoli equilateri, potremmo solo dividerlo in un numero dispari di triangoli equilateri, come mostrato in (b), che si divide in 5 triangoli equilateri più piccoli. Poiché non c’è modo di dividere il quadrilatero in un numero pari di triangoli, non possiamo dividerlo in 2 o 4 triangoli, quindi possiamo anche escludere n = 3 e n = 5.

Il caso per n = 4 è esposto nella domanda e quindi n = 4 è possibile. Il disegno (b) mostra il caso per n = 6. Uno qualsiasi dei triangoli equilateri più piccoli in questo disegno può essere suddiviso in 4 triangoli equilateri, che ha l’effetto di aggiungere 3 al numero totale di triangoli.  

Il disegno (c) è uno sviluppo di (b) con il triangolo superiore diviso in 4. Possiamo continuare in questo modo per creare disegni in cui n = 9, 12, 15, . . . . Pertanto, è possibile dividere il triangolo originale in n triangoli equilateri più piccoli dove n è un multiplo di 3, escluso n = 3.

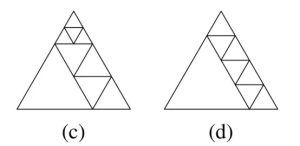
Tornando al disegno con n = 4, possiamo vedere che qualsiasi triangolo equilatero può essere diviso in 4 triangoli equilateri. Quindi, n può essere 7, 10, 13, . . . . Pertanto, è possibile dividere il triangolo originale in n triangoli equilateri più piccoli dove n è uno in più di un multiplo di 3.

Il disegno (d) mostra la divisione in 8 triangoli equilateri più piccoli, da cui possiamo mostrare che n = 11, 14, 17, . . . dividendo uno qualsiasi dei triangoli equilateri esistenti in 4 triangoli equilateri. Pertanto, è possibile dividere il triangolo originale in n triangoli equilateri più piccoli dove n è due in più di un multiplo di 3, escluso n= 5.

In conclusione, è possibile dividere il triangolo originale in n triangoli equilateri più piccoli per tutti i valori interi positivi di n, esclusi 2, 3 e 5.

A  lunedì prossimo.