
I Giochi del lunedì di prisma del 28 febbraio 2022 a cura di Fabio Ciuffoli
Questa settimana si svolgeranno on line i quarti di finale dei Campionati Internazionali di Giochi Matematici con la finale prevista a fine agosto 2022 a Losanna. Oggi proponiamo tre giochi che hanno fatto parte delle prove Junior Mathematical Olympiad, per i ragazzi della scuola primaria, del Regno Unito. Non pensate siano troppo facili, in particolare il terzo richiede una certa abilità di ragionamento, non solo matematico. Invitiamo i lettori a inviarci le loro osservazioni e proposte di soluzione nello spazio riservato ai commenti. Domani pomeriggio alle 17.00 pubblicheremo le soluzioni. A proposito, in bocca al lupo ai partecipanti!
Olimpiadi di Matematica Junior (JMO)
1. In questa somma di parole, ogni lettera rappresenta una delle cifre 0–9. Nessun numero inizia con 0. A quale cifra corrisponde ciascuna lettera?
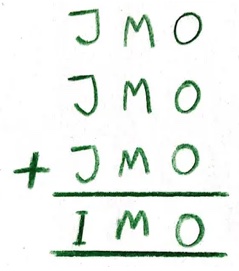
2. Nel diagramma seguente, un quarto di cerchio con raggio 3 cm è posizionato accanto a un quarto di cerchio con raggio 4 cm.
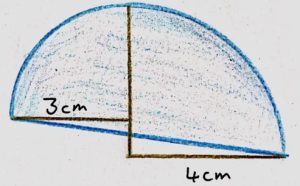
Qual è l’area ombreggiata totale delimitata dalle linee blu, in cm²?
3. Un triangolo equilatero è diviso in triangoli equilateri più piccoli.
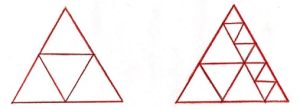
La figura a sinistra mostra che è possibile dividerlo in 4 triangoli equilateri. La figura a destra mostra che è possibile dividerlo in 13 triangoli equilateri. Quali sono i valori interi di n, dove n > 1, per i quali è possibile dividere il triangolo in n triangoli equilateri più piccoli?
Aggiornamento per le soluzioni click qui
I problemi sono tratti dalle prove Junior Mathematical Olympiad proposte da United Kingdom Mathematics Trust per l’anno 2019/20.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
18 risposte
1)
O = 0; M = 5; J = 1; I = 4. Oppure: O = 0; M = 5; J = 2; I = 7.
2) Con area cerchio/4 per entrambi i cerchi e le aree dei triangolini da aggiungere (a sinistra) e sottrarre (a destra), triangolini le cui basi sono rispettivamente 3 e 4 e le altezze 16/14 e 9/14, ottengo:
A = 25 Pi-greco – 1/2.
3) Infiniti triangoli equilateri. I primi possono essere:
1 (4^0), 4 (4^1), 16 (4^2), 64,…
Ma anche 13 (nell’esempio: 4 + 9); 4^2 + 9, 4^3 + 9……
Ma anche 4 + 9×4; 4 + 9 x 4^2, ….
Ottimo. Abbiamo pubblicato le soluzioni al link https://www.prismamagazine.it/giochi/33-soluzioni-del-28-febbraio-2022-olimpiadi-di-matematica-junior-in-uk/
1) La cifra delle unità è 0…la cifra delle decine è 5…la cifra delle centinaia è 2…quindi l’addendo che si ripete è 250.
3)Qualsiasi sia il valore del lato…tranne 1..il numero dei triangolini è un quadrato perfetto.
Bene la 1, oggi pomeriggio tutte le soluzioni con dimostrazione
Quesito 3: 4 è il numero minimo di triangoli equilateri più piccoli in cui un triangolo equilatero può essere scomposto. Consideriamo che se scomponiamo uno qualsiasi di questi 4 triangoli in altri 4 avremo 7 triangoli totali, ossia i 4 nuovi più i tre precedenti che non sono stati suddivisi. Se reiteriamo l’operazione a piacere, qualunque sia il numero di triangoli in cui il triangolo iniziale sia stato già scomposto, otterremo sempre un numero uguale al numero precedente più 3, ovvero aggiungeremo i 4 triangoli della ennesima scomposizione e sottrarremo 1 triangolo che è quello che è stato scomposto. Concludendo, la risposta è:
Tutti i numeri ( 1 + m ) dove m è multiplo di 3
Bene, la risposta non è del tutto completa. Questo gioco è interessante, anche se relativamente complesso, considerando che è stato somministrato nelle scuole primarie per le Olimpiadi di Matematica in UK. A domani per la soluzione.
Quesito n. 2: 19,13
Perfetto, matematica senza numeri. A domani per tutte le soluzioni.
Propongo queste soluzioni
Terzo esercizio
A domani per le soluzioni con dimostrazione
Perfetto.
19,38
Solleverei un dubbio sull’altezza dei due triangoli che tu hai dato pari a 0,5.
Provo a rispondere ai primi 2 quesiti.
1) Le lettere M e O possono essere associate solamente alle cifre 0 e 5. Tenendo conto dei riporti nella somma, si trova che la lettera O=0 e che la lettera M=5. Per la J esistono due soluzioni possibili J=1 e J=2. Pertanto I=4 se J=1 e I=7 se J=2.
2) Chiamo S4 l’area del quarto di cerchio di raggio 4, S3 l’area del quarto di cerchio di raggio 3, S2 l’area del rettangolo in basso a destra (non disegnato) di base 3 e altezza 4-3=1, S1 l’area del triangolo in basso (non disegnato) di base 7 e altezza 1. L’area richiesta, Scol = S4+S3+S2-S1. Utilizzando le formule trovo Scol=4*pi+9/4*pi+3-7/2=1/4*(25*pi-2)
Ottimo, a domani per tutte le soluzioni.
Le uniche cifre il cui triplo ha come cifra delle unità ancora la stessa cifra sono lo zero e il cinque (0+0+0=0 e 5+5+5=15). Dunque O e M devono essere tali cifre.
Siccome la colonna delle decine non cambia cifra nella somma, non deve ricevere riporto dalla colonna delle unità, dunque deve essere: O=zero e M=cinque
Se M=5 allora la colonna delle centinaia riceve un riporto di 1.
Dato che nel risultato manca la colonna delle migliaia, è necessario che J+J+J+1≤9 perciò J deve essere uguale a 2 e di conseguenza I=7
La mia risposta è : JMO=250 e IMO=750
P.S.: sarebbe bello se, prima della conferma del martedì pomeriggio, solo chi ha dato la sua risposta potesse vedere e interagire le risposte degli altri. E’ tecnicamente possibile farlo?
Ottimo. Sulla domanda relativa alla condizione “se solo chi a dato la sua risposta potesse vedere e interagire con le risposte altrui” giro la questione ai ns tecnici web.