
I Giochi del Lunedì di Prisma del 21 febbraio 2022 a cura di Fabio Ciuffoli
I quattro giochi, che proponiamo oggi, riguardano le aree ombreggiate nei disegni geometrici. Le immagini sono da studiare e osservare, finché non arriva il piacevole momento dell’intuizione. L’obiettivo degli autori è stimolare la riflessione sui diversi modi per risolvere problemi di geometria. Invitiamo i lettori a inviarci le loro osservazioni e proposte di soluzione nello spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni, indicando due modalità per ogni problema.
Ombra e luce
1. Un punto all’interno di un quadrato è collegato ai suoi quattro vertici. Quale frazione del quadrato è ombreggiata?
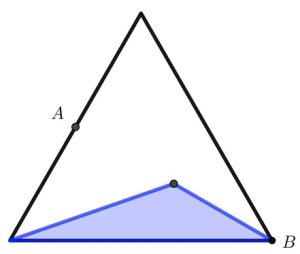
2. Una regione ombreggiata è costruita all’interno di un triangolo equilatero. A è il punto medio del lato, AB è bisettrice dell’angolo B e il punto interno è medio tra A e B. Quale frazione è ombreggiata?
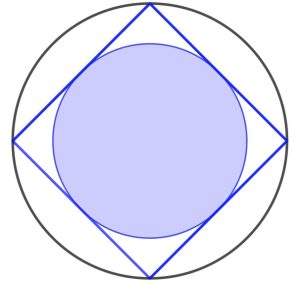
3. Un quadrato con il suo cerchio inscritto e circoscritto. Quale frazione del cerchio più grande è ombreggiata?
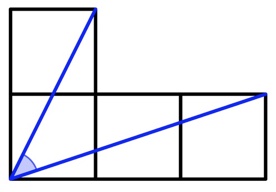
4. Quattro quadrati di dimensioni identiche sono disposti a L. Quanto misura l’angolo segnato in blu?
Aggiornamento per le soluzioni click qui
I problemi sono tratti dal bel libro More Geometry Snacks di Ed Southall e Vincent Pantaleoni.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
17 risposte
Le mie soluzioni
Bellissime. Al link sopra, dove è scritto click qui, trovi altre soluzioni possibili.
Fuori tempo massimo, ma non ho guardato le risposte altrui, nè le soluzioni:
1) 1/2, sia per confronto di due coppie di figure equivalenti, che con costruzione geometrica. tracciando due segmenti // a due lati del quadrato si vede che basi e altezze dei triangoli sono congruenti a due a due.
2) 1/4: la bisettrice del triangolo equilatero lo divide in due parti congruenti, per cui BA col vertice in alto è metà triangolo equilatero.
Il punto interno divide AB in due segmenti uguali, “basi” dei due triangolini. Siccome AB è bisettrice, nel triangolo equilatero, è anche altezza, per cui dal vertice in basso a sinistra (comune ad entrambi i triangolini) parte un’altezza coincidente ad entrambi (fino al punto B).
I due triangolini hanno pertanto stessa base e stessa altezza, sono pertanto equivalenti, e si spartiscono la metà area restante, dunque 1/2 di 1/2 = 1/4.
3) 1/2: nel sia a l’apotema (raggio minore) e r il raggio maggiore. Facendo il rapporto tra le aree, sostituendo r con a rad.2, si ottiene 1/2.
4) 45°: si costruisce un triangolo unendo le “estremità” libere dei lati dei triangoli.
Per costruzione si nota che i due lati sono congruenti (ipotenuse di triangoli di cateti 1 e 2).
I tre lati formano un triangolo rettangolo nel vertice in alto coi cateti congruenti, pertanto il triangolo è anche isoscele e l’angolo ricercato è quindi 45°.
Chiedo conferma di lettura per non aver scritto invano 😉
Ottimo. Al link sopra, presentiamo le soluzioni con due metodi differenti per ciascun problema.
1 Triangoli colorati e triangoli non colorati sono congruenti…per cui 1/2.
2) 1/4.
3) 1/3.
4) Unendo due punti si ottiene un triangolo rettangolo isoscele..per cui l’angolo misura 45 gradi.
Bene, non concordo sulla tua risposta al 3. A più tardi per le soluzioni.
Qualche tentativo di soluzione alternativa a quelle già proposte…
Ottimo. A domani per le soluzioni.
Penso non serva aggiungere altro per rispondere che l’angolo misura 45°
Ottimo. Aggiungo solo, per chi avesse voglia di cercarli, che per ogni problema sono possibili due metodi risolutivi. A domani per le soluzioni.
Terzo gioco:
Chiamiamo R il raggio della circonferenza esterna ed r il raggio della circonferenza interna. Abbiamo che la diagonale del quadrato vale 2R, perciò il lato vale R√2. Esso è uguale a 2r, da cui r=(R√2)/2. Il rapporto tra le aree è dunque (π r²)/(π R²) cioè semplicemente il rapporto tra il quadrato dei raggi: [(R√2)/2]² / R² = 1/2 R²/R² =1/2.
Nel secondo quesito il rapporto vale 1/4: congiungendo A con B si divide il triangolo equilatero in 2 triangoli rettangoli congruenti; chiamando C il vertice in basso a sinistra ed M il punto medio di AB si ha che i triangoli CAM e CMB hanno le basi congruenti che appartengono alla stessa retta AB (per ipotesi) e il terzo vertice in comune, pertanto anche le altezze relativale ad AM e BM sono congruenti e quindi l’area di CMB è uguale a quella di CAM, cioè 1/2 di CAB che vale 1/2 dell’area totale. 1/2 × 1/2 = 1/4
(A patto che il punto all’interno del quadrato non sia casuale ma si trovi sulla diagonale, come si vede nel disegno)
Non c’è alcun vincolo che il punto si trovi sulla diagonale!
Va bene, allora devo pensarci un po’ meglio, grazie mille per la risposta
Correzione: la somma delle altezze dei triangoli ombreggiati è uguale al lato del quadrato. L’area vale dunque quanto l’area di un triangolo che ha per base e per altezza l, cioè l²/2. Dato che l’area totale è l’area del quadrato, cioè l², il rapporto vale (l²/2)/l² cioè 1/2. Molto carino questo quesito!
Il primo è immediato, l’area ombreggiata è uguale all’area “bianca” perché i triangoli sono congruenti a due a due, dato che hanno la base congruente e il terzo vertice in comune. Pertanto il rapporto vale 1/2.