Menu
Le soluzioni del 21 febbraio 2022 a cura di Fabio Ciuffoli
Nella mattinata di ieri abbiamo proposto quattro problemi di geometria e ora pubblichiamo le soluzioni presentando due differenti metodi per ciascun problema.
Ombra e luce – soluzioni
1. Un punto all’interno di un quadrato è collegato ai suoi quattro vertici. Quale frazione del quadrato è ombreggiata?
1. SOLUZIONE. ½.
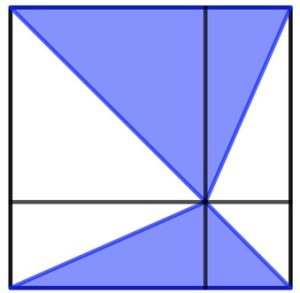a. Segmentando il quadrato in questo modo, si può vedere che metà di ogni area interna è ombreggiata.
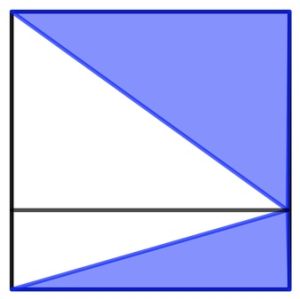b. Tracciamo un segmento parallelo alla base e passante per il punto. L’illustrazione mostra che i due triangoli ombreggiati sono rispettivamente uguali ai due triangoli in chiaro.
2. Una regione ombreggiata è costruita all’interno di un triangolo equilatero. A è il punto medio del lato, AB è bisettrice dell’angolo B e il punto interno è medio tra A e B. Quale frazione è ombreggiata?
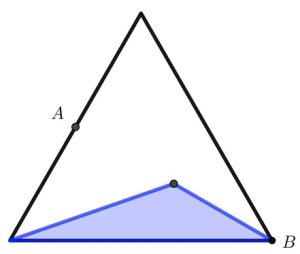
2. SOLUZIONE. ¼
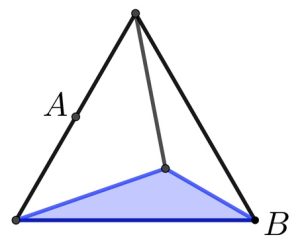a. Disegniamo la linea dal vertice superiore del triangolo ombreggiato al vertice superiore del triangolo equilatero. Il triangolo bianco più grande ha un’area che è metà dell’area del triangolo equilatero, poiché ha la stessa base ma metà dell’altezza. I restanti due triangoli sono congruenti, quindi hanno ciascuno un’area un quarto del triangolo equilatero.
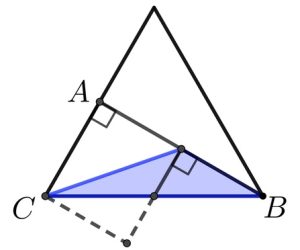b. Disegniamo un rettangolo come mostrato. L’area del triangolo ombreggiato è metà dell’area di quel rettangolo, poiché l’area ombreggiata al di fuori del rettangolo è uguale all’area delimitata dalla linea tratteggiata. L’area del rettangolo (AC x 1/2AB corrisponde a metà della base x metà dell’altezza del triangolo equilatero) è quindi metà dell’area del triangolo equilatero.
3. Un quadrato con il suo cerchio inscritto e circoscritto. Quale frazione del cerchio più grande è ombreggiata?
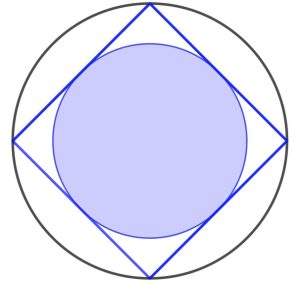
3. SOLUZIONE. ½.
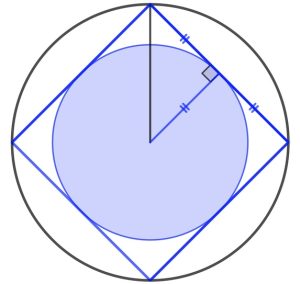a. Definiamo R il raggio del cerchio grande e r il raggio del cerchio piccolo. Tracciamo un triangolo rettangolo con l’ipotenusa R e gli altri due lati r. Per il teorema di Pitagora, avremo R2 = r2 + r2; R2 = 2r2; r2 = R2 /2. Poiché l’area di un cerchio è π volte il raggio al quadrato, l’area ombreggiata deve essere metà dell’area del cerchio grande.
b. Le aree del quadrato azzurro e del rettangolo grigio che sono uguali, possono essere calcolate in due modi. Usando il raggio r risulta (2r)2 = 4r2. Usando il raggio R, che è una mezza diagonale ma anche metà base del rettangolo grigio è 2R2. Questi termini sono uguali, quindi di nuovo 4r2 = 2R2 da cui r2 = R2 / 2.
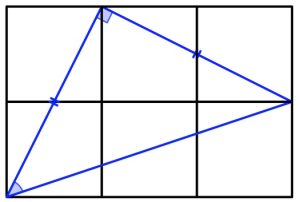
4. Quattro quadrati di dimensioni identiche sono disposti a L. Quanto misura l’angolo segnato in blu?
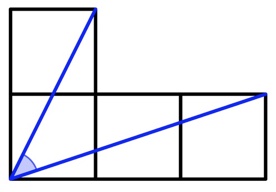
4. SOLUZIONe. 45°.
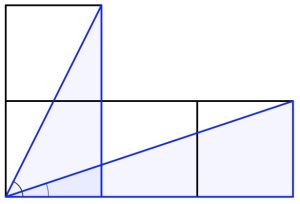
a. Questa è la dimostrazione più bella: non servono parole!
b. E’ possibile, con la trigonometria, calcolare gli angoli opposti ai cateti minori dei due triangoli rettangoli rispettivamente con cateti 1 e 3 e cateti 1 e 2. Il risultato si ottiene sommando il valore degli angoli e sottraendo questa somma a 90.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
I problemi di geometria si rivelano sempre stimolanti e coinvolgenti, come dimostrato dagli ottimi commenti su questo blog. Ho ricevuto anche altri diversi contributi e vorrei segnalarne un paio:
per il problema n. 1, Silvana Andreoli: “Indicando con x l’altezza del triangolo in basso, la sua area è l*x/2; l’area del triangolo in alto è l*( l-x)/2; semplificando si ottiene l^2/2, ossia la metà dell’area del quadrato.”
Per il problema n. 2, Matteo Scala: “Usando un po’ di trigonometria l’area colorata è (L x L (sqrt3)/4) x sin (30) /2. Considerando che l’espressione dentro parentesi è l’area del triangolo equilatero, la frazione è dunque ¼.”
Grazie a coloro che hanno partecipato.