
I giochi del lunedì di Prisma del 6 dicembre 2021 a cura di Fabio Ciuffoli
Ogni anno, l’interessante sito web di matematica Mathigon propone un originale Calendario dell’Avvento, pubblicando un problema al giorno dall’1 al 24 dicembre. Abbiamo selezionati tre giochi che proponiamo di seguito. Invitiamo i lettori a presentarci osservazioni e proposte di soluzione nello spazio riservato ai commenti. Alle ore 17.00 di domani pubblicheremo le soluzioni.
Un originale Calendario dell’Avvento
1. Sei cerchi, di raggio 1, sono disposti con i centri sui vertici di un esagono regolare. Qual è l’area dello spazio scuro delimitato dai cerchi?

2. E’ possibile piantare 7 alberi su 6 linee rette, contenenti 3 alberi ciascuna?

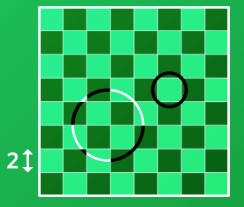
3. Quanto misura il raggio del cerchio più grande, che si può disegnare sulla scacchiera, con la circonferenza che giace interamente su quadrati neri? Ogni quadrato ha il lato lungo 2.
Aggiornamento per le soluzioni click qui
I giochi, proposti oggi, sono tratti dal sito web Mathigon che consigliamo di visitare. E’ un bellissimo sito gratuito, di divulgazione matematica dove si trovano ottime animazioni interattive e altre iniziative meravigliose e intelligenti.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
16 risposte
Io dico 1 (area dell’esagono con lato 2) meno (area di sei settori circolari di 120 gradi del cerchio di raggio 1) che viene 4,1 circa
2 non mi viene con 6 linee??
3. Concordo con le soluzioni giá presentate da Gianpaolo
Bene il primo e anche il terzo. Per il secondo, alle 17.00 pubblicheremo la soluzione con un disegno.
1) 5,76 circa
3) 1,4 circa
Non è così. A oggi pomeriggio per le soluzioni e per un eventuale confronto.
Interessanti i giochi di questa settimana, grazie! Concordo con la soluzione già indicata per il primo. Non ho avuto ancora un’ispirazione per il secondo però mi sono divertito con quello degli alberi (per un po’ ho pensato che la risposta fosse no, non è possibile) di cui allego un’immagine.
Per il problema degli alberi posso dirti che occorre disegnare un triangolo… Per il problema della scacchiera e del cerchio, è già stata proposta la soluzione corretta, anche se con un disegno risulterebbe maggiormente comprensibile. Grazie a te. Oggi pomeriggio le soluzioni con i disegni.
Area parte cerchi interna all’esagono formato unendo i centri del cerchio: 6π/3 = 2π
Area esagono = 2pa/2 = (2x6x√3)/2 = 6√3
Area richiesta = 6√3 – 2π
Scacchiera: centrare su casella nera, con apertura √10
Alberi allineati: son fermo a 5 rette…
Bene 1 e 3. Sul 2 consiglio di impostare un disegno a partire dai commenti precedenti … A domani per le soluzioni.
Per Virginio: molto bene. A domani.
3) r=radq(10) con centro nel centro di una casella nera “abbastanza lontana” dal bordo (8 posizioni possibili)
Ottimo, a domani per le soluzioni con dimostrazione.
1) L’area dello spazio scuro interno delimitato dai cerchi è 2*(3sqrt(3)-pigreco) = circa 4,109119538
2) Sì, è possibile avere 7 alberi su 6 linee rette, contenenti ciascuna 3 alberi. Si abbia un triangolo equilatero ABC, con incentro G (che è anche ortocentro, baricentro e circocentro) e si costruisca all’interno un altro triangolo equilatero DEF (con i punti D, E, F posti a metà rispettivamente dei lati AB, BC e CA. Basta piantare i 7 alberi nei punti A B C D E F G.
3) Non si capisce come possa una circonferenza giacere interamente su quadrati neri, a meno che sia inscritta in un solo quadratino nero. Quindi r=1.
Bene 1 e 2. Sul 3, c’è un raggio maggiore di 1. A domani per le soluzioni con dimostrazione
OK, per il terzo, r=RADQ(2)
Non proprio (se ho letto bene).
Hai ragione, r = RADQ(1^2+3^2) = RADQ(10) circa 3,162