
Le soluzioni del 6 dicembre 2021 a cura di Fabio Ciuffoli
Ieri mattina abbiamo proposto tre problemi tratti dal sito web Mathigon, dove si trova un originale Calendario dell’Avvento di giochi logici e matematici e ora presentiamo o le soluzioni.
Un originale Calendario dell’Avvento – soluzioni
1. Sei cerchi, di raggio 1, sono disposti con i centri sui vertici di un esagono regolare. Qual è l’area dello spazio scuro delimitato dai cerchi?

1. SOLUZIONE. Colleghiamo i centri di tutti i cerchi e otteniamo un esagono regolare di lato 2. Ci sono molti modi per calcolare l’area degli esagoni regolari, ad esempio suddividendoli in sei triangoli equilateri. L’altezza di uno di questi triangoli è √3, quindi l’area dell’esagono è 6 (2√3)/2 = 6√3. Ora ogni angolo interno di un esagono regolare è di 120° e perciò un terzo di ogni cerchio è interno all’esagono. L’area di un cerchio è πr2 = π. L’area scura si ottiene per differenza tra area dell’esagono e area dei 6 settori circolari: 6√3 – 6 (1/3) π = 6√3 – 2π ≈ 4,1.
2. E’ possibile piantare 7 alberi su 6 linee rette, contenenti 3 alberi ciascuna?

2. SOLUZIONE. Sì, è possibile! Gli alberi vanno disposti su un triangolo equilatero, con uno al centro.

3. Quanto misura il raggio del cerchio più grande, che si può disegnare sulla scacchiera, con la circonferenza che giace interamente su quadrati neri? Ogni quadrato ha il lato lungo 2.
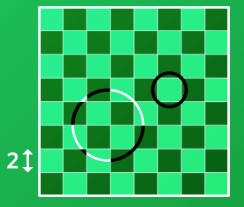
3. SOLUZIONE. Una volta trovata la posizionare il cerchio, non è difficile calcolare il raggio. Con il teorema di Pitagora, se ogni quadrato ha il lato 2, avremo: r2 = 12 + 32 = 10 quindi r =√10 ≈ 3,16.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
2 risposte
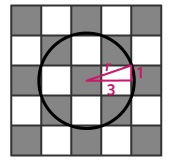
Sul problema 3, vorrei segnalare anche la soluzione, corredata da un disegno, proposta da Riccardo Montorzo.
“Prendiamo un quadrato nero. La circonferenza deve passare per due vertici altrimenti esce su un quadrato bianco. I due vertici possono essere gli estremi del lato d’un quadrato o d’una diagonale. Se sono tutti vertici di un lato si ha la circonferenza riportata nella foto. Se in un quadrato sono i vertici di una diagonale da essi la circonferenza esce in altri quadrati neri nei quali deve passare per i vertici di un lato altrimenti passerebbe su 3 punti allineati. Quindi l’incrocio degli assi delle corde dà il centro. Un disegno spiega meglio.”
Tra le proposte di soluzione al problema 3, che mi sono arrivate, vorrei segnalare il seguente simpatico confronto tra due lettori.
Alessandro Buggiani: Gli spigoli [vertici] tra bianco e nero non possono considerarsi esclusivamente neri, quindi qualsiasi linea che passi per gli spigoli [vertici] non giace interamente su quadrati neri. L’unica possibile è r = 1.
Nicola Fusco: Una linea è unidimensionale quindi può passare da un quadrato nero ad un altro nero senza toccare alcun punto bianco.
Alessandro Buggiani: Secondo questa logica non tocca neanche nessun punto nero, quindi non rispetta quel “esclusivamente “ [interamente]. Anche il punto zero dimensionale di contatto dei vertici è da ritenere bianco o nero? O terra di nessuno! comunque è lana caprina! Qualunque sia la soluzione quella linea ideale di circonferenza deve passare per quei vertici nero-nero.
Nicola Fusco: Una volta che definisci una tassellazione del piano in quadrati devi decidere, per ogni quadrato su quali lati è “chiuso” e su quali è “aperto”. Una volta fatta una scelta uguale oer tutti (ad esempio ogni quadrato contiene il lato inferiore e quello destro ma non contiene quello superiore e quello sinistro) si può sempre passare da un quadrato nero ad un altro nero senza passare per un punto di un quadrato bianco e viceversa
Alessandro Buggiani: Il problema nasce sui vertici. Non tanto sui lati. Tendenzialmente dovresti scendere alle dimensioni o molto vicino a quelle di Plank.
Nicola Fusco: Non mettiamo in mezzo cose che non centrano. I vertici fanno parte dei segmenti, quindi fanno parte o non fanno parte di questo o quel quadrato. Nell’esempio che ho fatto, ogni quadrato contiene sicuramente il vertice in basso a destra e diciamo che contiene anche quello in basso a sinistra. In questo modo, ripeto, qualunque curva può passare da nero a nero senza attraversare il bianco.