
I Giochi del Lunedì di Prisma del 6 maggio 2024 a cura di Fabio Ciuffoli
L’antico Gioco del Nim, di origine orientale, è uno dei giochi più vecchi e intriganti oggi conosciuti. Si gioca in due giocatori disponendo un numero variabile di oggetti (fiammiferi, carte da gioco, monete o altro) su più file. I giocatori a turno tolgono uno o più oggetti da una fila e vince chi ritira l’ultimo oggetto. Come è facile intuire, esistono numerose varianti che si differenziano per numero di file, di oggetti per ciascuna fila e anche per l’esito finale: si potrebbe stabilire che perde chi è costretto a ritirare l’ultimo oggetto. Proponiamo di seguito quattro partite, con varie disposizioni iniziali e anche con un diverso esito finale nel problema Marienbad e invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio relativo ai commenti. Domani pomeriggio alle ore 17.00 pubblicheremo le nostre risposte commentate.
Il Gioco del Nim
1. In una partita, con la disposizione iniziale su tre file rispettivamente con 1 – 3 – 5 oggetti, come proposto in figura, vince chi ritira l’ultimo oggetto. Sapreste individuare chi è sicuro di vincere, il primo o il secondo giocatore? E con quale strategia? 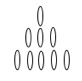
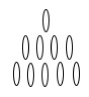
2. In una partita Nim con la disposizione iniziale su tre file rispettivamente con 1 – 4 – 5 oggetti, come disegnato in figura, vince chi ritira l’ultimo oggetto. Sapreste individuare chi è sempre sicuro di vincere, il primo o il secondo giocatore e con quale strategia?
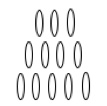
3. In una partita Nim con la disposizione iniziale su tre file rispettivamente con 3 – 4 – 5 oggetti, come in figura, vince chi ritira l’ultimo oggetto. Sapreste individuare chi è sempre sicuro di vincere, il primo o il secondo giocatore e con quale strategia?
4. L’anno scorso a Marienbad chi inizia perde sempre! Il Gioco del Nim è diventato popolare attraverso il film di Alain Resnais “L’anno scorso a Mariembad” Leone d’oro al Festival di Venezia 1961. Il protagonista X, interpretato da Giorgio Albertazzi, viene sfidato da un impassibile sconosciuto M, che lo batte sempre. Riportiamo un dialogo dal film.
M: ” Conosco un gioco in cui vinco sempre”.
X: “Se non potete perdere, non è un gioco”.
M: “Posso perdere ma vinco sempre”.
M: “Si gioca in due. Le carte si dispongono in questo modo: 1 – 3 – 5 – 7. Ciascun giocatore prende le carte, quando è il suo turno. Quante carte vuole purché ne prenda da una sola fila alla volta. Quello a cui resta l’ultima carta … ha perduto. Volete cominciare voi?”
In figura proponiamo la situazione iniziale delle 16 carte.
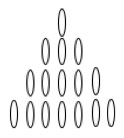
Sapreste spiegare perché il signor M vince sempre?
Aggiornamento per le soluzioni click qui.
Per chi volesse esercitarsi e mettersi alla prova, segnaliamo l’ottimo sito BASE Cinque di Gianfranco Bo che mette a disposizione un programma per giocare con il computer e con un’adeguata strategia si può battere il computer.
http://utenti.quipo.it/base5/jsmarienbad/jsmarienbad.htm
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
8 risposte
La strategia per vincere una partita a Nim è questa:
Scrivere in binario il numero di oggetti per riga
Sommare in modo esclusivo (XOR) i numeri ottenuti
Se la somma XOR non è 0 il giocatore di turno può vincere se agisce su una della righe in modo che l’avversario riceva righe a somma XOR 0
Il giocatore che riceve uno schema a somma XOR 0 non può che restituire una somma XOR diversa da 0
Metto qui le mie proposte
Premessa: nel gioco del Nim vince chi prende l’ultimo oggetto
Gioco 1: 1-3-5 Il primo giocatore è sicuro di vincere se gioca razionalmente
Come prima mossa toglie 3 oggetti dalla terza riga
Gioco 2: 1-4-5 Se il secondo giocatore gioca razionalmente vince
Gioco 3: 3-4-5 Il primo giocatore è sicuro di vincere se gioca razionalmente
Come prima mossa toglie 2 oggetti dalla prima riga
Premessa: nel gioco del Marienbad perde chi prende l’ultimo oggetto
Gioco 4: 1-3-5-7 Il primo giocatore vince se gioca razionalmente ovvero se lascia sul campo un numero pari di righe con un solo oggetto In questo caso inizia bene se rimuove 2 da 3 oppure 4 da 5 oppure 6 da 7
Questa è la parte che ritengo corretta
Gioco 4: 1-3-5-7 Il primo giocatore vince se gioca razionalmente ovvero se lascia sul campo all’avversario un numero dispari di righe con un solo oggetto In questo caso inizia bene se rimuove 3 oppure 5 oppure 7
Questa è la parte da rimuovere
Gioco 4: 1-3-5-7 Il primo giocatore vince se gioca razionalmente ovvero se lascia sul campo un numero pari di righe con un solo oggetto In questo caso inizia bene se rimuove 2 da 3 oppure 4 da 5 oppure 6 da 7
Gioco n 2 Questa è la classica perdente per chi muove:
a) 1.1 1.3!
b) 1.2 3.3!
c) 2.2 5.3!
d) 3.2 2.3!
e) 4.2 5.3!
f) 1.3 1.1!
g) 2.3 2.2!
h) 3.3 1.2!
i) 4.3 4.2!
j) 5.3 3.2!
Con la 1,4,5 è semplice rispondere:
o si generano due file dello stesso numero di monete, oppure si genera la 1,2,3 che è posizione vinta. Questa è più difficile: (9,8,7,3,2,7)
Quarto quesito – Dipende dagli oggetti che ci sono a disposizione se sono pari vince il primo che gioca se è dispari vince il secondo.
Gioco 4
0001
0011
0101
0111
Colonne pari, il primo che gioca ha già perso.
Gioco 2 Perde chi tira per primo
n. 3. Il primo giocatore qui è sicuro di vincere. La prima mossa è togliere 2 alla prima riga