
I Giochi del Lunedì di Prisma dell’11 marzo 2024 a cura di Fabio Ciuffoli
Oggi presentiamo quattro problemi considerati degli evergreen del problem solving che, seppure non recenti, sono sempre stimolanti e suggestivi. I primi due trattano la dissezione e l’assemblaggio di una tavola di legno mentre il terzo e il quarto sono relativi alla lunghezza di una corda avvolta attorno a un cilindro. Il terzo problema è stato originariamente proposto in un esame per studenti diciottenni, in 16 paesi, con risultati abbastanza sorprendenti, che riportiamo in calce. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le nostre proposte di soluzione.
Un quadrato e un cilindro con la corda attorno
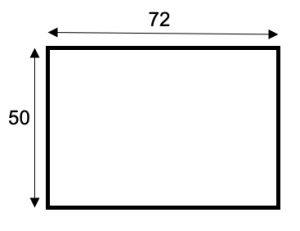
1. Un falegname vuole ottenere una tavola di legno quadrata che misura 60 cm per 60 cm, ma nel suo laboratorio ha solo una tavola rettangolare di 50 cm per 72 cm. Come è possibile tagliare il legno in due pezzi, in modo che possano essere incollati insieme, per formare la tavola quadrata desiderata?
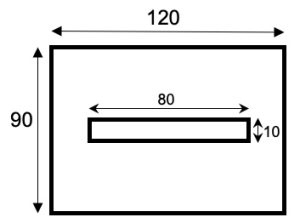
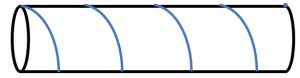
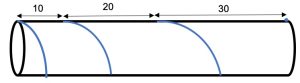
4. Una corda è avvolta regolarmente intorno a un cilindro di diametro 14 cm compiendo tre giri completi. Il primo giro si completa a 10 cm dalla base, il secondo giro si completa a 20 cm dal primo e il terzo a 30 cm dal secondo, come disegnato in figura. Quanto è lunga la corda?
Aggiornamento per le soluzioni click qui.
Il terzo problema è stato originariamente proposto venticinque anni fa in un esame per studenti diciottenni, in 16 paesi, che studiavano matematica “avanzata” di livello A (corrispondente all’esame di maturità in Italia). È stata una delle domande più difficili del test, con solo il 10% degli studenti che hanno dato la risposta giusta. Il Paese con risultati migliori è stato la Svezia, dove il 24% ha risposto correttamente. Negli Stati Uniti e in Francia, il punteggio è stato di un misero 4%. L’Italia non ha partecipato. Il problema, tuttavia, è piuttosto bello e non richiede matematica superiore a quella insegnata nelle scuole medie dagli 11 ai 14 anni.
Nell’immagine in evidenza: Falegname di Kazimir Malevich (1929)
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
8 risposte
Vedi disegno.
Problemi 3 e 4. Vedi immagine allegata
3. 40 cm.
4. sqrt(100+196PI^2) + sqrt(400+196PI^2) +sqrt(900+196PI^2) = ~146.66 cm.
Ottimo e chiarissimo, come sempre.
Problema n. 4. Vedi disegno.
Problemi 3 e 4.
Credo che questo tipo ti problemi si risolva considerando che per un giro completo (che, quindi, interessi un’intera circonferenza C) su un’altezza pari ad H, immaginando di “srotolare” il cilindro di diametro C/2/pi e altezza H la corda diventi la diagonale del rettangolo risultante, di lati C e H, con lunghezza sqrt(C^2+H^2).
Nel primo caso, quindi abbiamo 4 avvolgimenti su 4 porzioni del cilindro di altezza 24/4 cm = 6 cm, e la lunghezza e’ sqrt(6^2+8^2) * 4 cm = 40 cm.
Nel secondo caso, invece, abbiamo 4 avvolgimenti su circonferenze C = 14*pi cm e altezze 10 cm, 20 cm e 30 cm rispettivamente, per cui la lunghezza e’ sqrt(10^2+14^2*pi^2) + sqrt(20^2+14^2*pi^2) + sqrt(30^2+14^2*pi^2) cm = sqrt(100+196*pi^2) + sqrt(400+196*pi^2) + sqrt(900+196*pi^2) cm = 2 * [ sqrt(25+49*pi^2) + sqrt(100+49*pi^2) + sqrt(225+49*pi^2) ] cm = 146.660 cm
Se le mie reminiscenze non mi ingannano, volendo usare le equazioni parametriche di una curva, utilizzando come parametro l’angolo phi, avremmo per un giro completo (0<=phi L = int_0^(2pi) dphi sqrt(x'(phi)^2+y'(phi)^2+z'(phi)^2) = int_0^(2pi) { dphi sqrt[ R^2 sin^2(phi) + R^2 cos^2(phi) + H^2/(4pi^2) ] } = int_0^(2pi) { dphi sqrt[ R^2 + H^2/(4pi^2) ] } = 2 pi sqrt[ R^2 + H^2/(4pi^2) ] = sqrt[ 4 pi^2 R^2 + H^2 ], dove l’apice indica la derivata prima rispetto al parametro phi che descrive la curva.
Problema 1. Fatto a volo! Figura non perfetta
Soluzione ingegnosa, ma si chiede di tagliare il legno in due pezzi e quindi non va bene. A domani per le soluzioni.