
10. I giochi del lunedì di Prisma 13 settembre 2021 a cura di Fabio Ciuffoli
Questa settimana studenti e insegnanti tornano in aula. E’ un nuovo “capodanno della scuola” – come è stato detto – che porta con sé aspettative, desideri, speranze e anche qualche timore. I giochi di oggi prendono spunto dal lavoro di Catriona Shaerer, insegnante e appassionata divulgatrice, che propone stimolanti problemi di geometria risolvibili senza algebra. Catriona, con il suo “laboratorio-scuola”, ci stimola a scomporre e ricomporre le figure per vedere nuove soluzioni.
Invitiamo i lettori a presentarci osservazioni e proposte di soluzione nello spazio riservato ai commenti. Alle ore 17.00 di domani pubblicheremo le soluzioni.
Gli enigmi colorati di Catriona
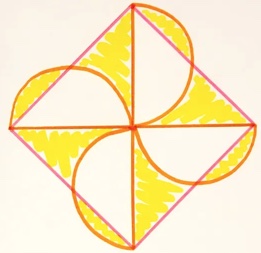
1. Spicchi arancioni. Se il raggio di ogni semicerchio è 5 cm, qual è l’area ombreggiata in giallo totale?
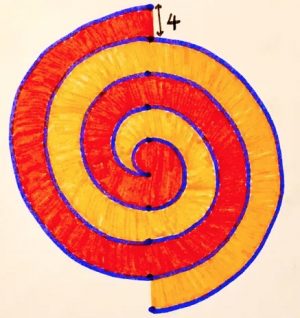
2. Doppia spirale. Dieci punti, equidistanti 4 cm l’uno dall’altro, sono uniti da semicerchi e formano la seguente spirale. È maggiore l’area rossa o arancione? E di quanto?
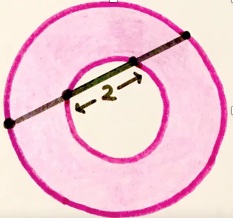
3. La ciambella rosa. I quattro punti, sulle due circonferenze, sono equidistanti di 2 cm. Qual è l’area ombreggiata?
I giochi di oggi, opportunamente rielaborati, sono tratti dal libro Geometry Puzzle di Catriona Shearer.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
7 risposte
Bel dibattito… Come già dimostrato il problema 1 =100 cmq
Problema 2 = area rossa più grande di un cerchio con raggio 2
Problema 3 = area rosa 8pigreco
Mi astengo dal pubblicare i disegni…
Ok a domani per le soluzioni. Concordo Sul bel dibattito.
Poco da aggiungere all’ottimo commento di Daniele. Pensando a Catriona, forse per il problema due, è possibile una soluzione più semplice. Le posizione dei punti, equidistanti sulle due circonferenze, potrebbero considerarsi generiche e quindi spostabili in un punto conveniente come il diametro, allora avremmo due cerchi: il piccolo di raggio 1 e l’altro di raggio 3. A questo punto è facile calcolare l’area rosa come differenza tra le due aree.
Grazie per l’apprezzamento 🙂
Se l’ho interpretato correttamente, il secondo commento apre un tema che ho toccato molte volte, e che suscita sempre focose diatribe! È necessario dimostrare l’indipendenza di un problema da un dato (perché altrimenti il problema non sarebbe risolubile), oppure si può “furbamente” inferire questa informazione da come il problema è formulato? Nel caso particolare: posso assumere che i quattro punti stiano sul diametro delle circonferenze, assumendo che il risultato non cambi?
Faccio un altro esempio. Se volessi dimostrare che la somma degli angoli interni di un triangolo è pari a 180°, posso limitarmi a considerare un triangolo equilatero (perché il problema lascia intendere che il risultato non dipende dalla forma del triangolo) oppure devo trovare una dimostrazione che valga per un triangolo qualsiasi?
Su questa domanda, ho visto opinioni molto contrastanti. In molti apprezzano lo spunto intuitivo di capire che un dato non è necessario, e costruire il caso particolare che porta ad una soluzione più semplice è un bell’esercizio. I detrattori di questa tecnica sostengono invece che non sia un procedimento completo, e che anzi la dimostrazione dell’invarianza del risultato rispetto alla configurazione scelta sia l’essenza stessa del problema.
OK, chiedo scusa se mi sono lasciato prendere la mano, spero il mio commento non sia preso in modo critico: siamo qui per divertirci con questi giochi matematic!
D’accordissimo, i giochi offrono ottimi spunti per ragionare sui metodi: empirico induttivi, teorico deduttivi e anche altri. Ottima discussione. Sommessamente, propongo una citazione sulla gioia della scoperta che riguarda anche i giochi:
“Una grande scoperta risolve un grande problema, ma c’è un granello di scoperta nella soluzione di ogni problema. Il nostro problema potrebbe essere modesto, ma se sfida la nostra curiosità e mette in gioco le nostre facoltà inventive, e se lo risolviamo da soli, possiamo sperimentare la tensione, la gioia e il trionfo della scoperta.”
G. Polya (1887 – 1985) La scoperta matematica
Ottima citazione 🙂
La raccolta di Catriona Shearer è incredibile, una delle più belle che abbia mai visto, ottima scelta. Allego le mie proposte di soluzione.