
Le soluzioni del 6 settembre 2021 a cura di Fabio Ciuffoli
Ieri mattina abbiamo proposto tre problemi, prendendo spunto dai sangaku e dalla geometria e ora presentiamo le soluzioni.
Geometria e Sangaku – soluzioni
1. Quattro esagoni regolari concentrici sono equidistanti dal punto centrale ovvero le distanze, a partire dal centro, tra il primo e il secondo esagono, tra il secondo e il terzo e tra il terzo e il quarto, sono uguali. Quale frazione dell’area dell’esagono più grande è ombreggiata?

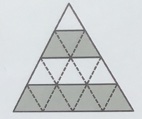
Un altro modo ancora: se ipotizziamo l’area dell’esagono centrale uguale a uno, le aree degli altri esagoni saranno rispettivamente 2², 3² e 4². Avremo quindi (4² – 3² + 2² -1) / 4² = 10/16 = 5/8.
[Ricordiamo la formula per calcolare l’area di un triangolo equilatero, conoscendo il lato: (√3/4) * L², dove L è la misura del lato].
2. All’interno del quarto di cerchio di raggio 6, ci sono due semicerchi e un cerchio, ciascuno tangente agli altri. Quanto misurano i raggi del cerchio nero e del semicerchio nero più piccolo?
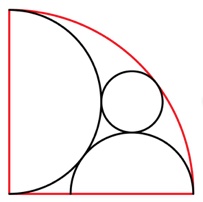
2. SOLUZIONE. Definiamo r il raggio del cerchio e R il raggio del semicerchio più piccolo e poiché il quarto di cerchio ha raggio 6, il raggio del semicerchio più grande è 3. Proponiamo due metodi di soluzione.
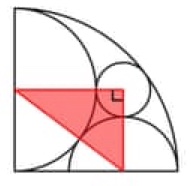
Metodo 1. Consideriamo il triangolo rettangolo sopra. L’ipotenusa è 3 + R, il cateto maggiore è r + 3 e quello minore è 3. Con il teorema di Pitagora avremo:
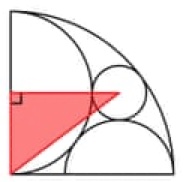
Metodo 2. Consideriamo il triangolo rettangolo sopra. L’ipotenusa è 6 – r, il cateto maggiore è 3 + r e quello minore è 3. Con il teorema di Pitagora avremo:
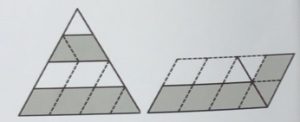
3. Quattro semicerchi con raggio 2 sono costruiti nel quadrato rosso sottostante. Qual è l’area del quadrato?
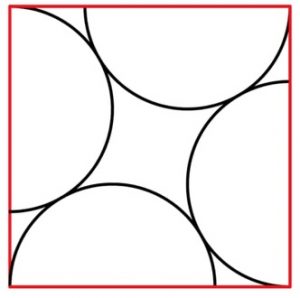
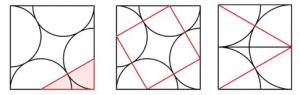
3. SOLUZIONE. Presentiamo due metodi.
Metodo A. Il triangolo, nell’immagine in basso a sinistra, ha ipotenusa 4 e cateto minore 2. Indicando con x il cateto maggiore avremo:
Metodo B. Nell’immagine centrale sotto, con un quadrato rosso all’interno del quadrato originale, possiamo riorganizzare i triangoli all’esterno di quel quadrato rosso per creare un rettangolo, disegnato sotto a destra, che ha i lati 2√3 e 4. L’area del quadrato grande è data dall’area del quadrato più piccolo sommata all’area del rettangolo:
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
7 risposte
Ecco il seguito
Ottimo, mi guarderò con calma tutti i passaggi. Ho girato la richiesta di inserire file PDF al programmatore. Interessante il riferimento alla domanda 6 del test di medicina 2021. Grazie per il contributo.
Ecco la mia dimostrazione
(invio due commenti, per caricare due immagini)
[sarebbe bello poter caricare pdf]
Mi associo a Ste, in quanto solo quella dimostrazione garantisce l’ unicità della soluzione.
Grazie
La risposta a Stè dovrebbe aver chiarito che, sicuramente almeno in questo caso , i due triangoli sono rettangoli.
In relazione al problema 2, propongo metodi di soluzione alternativi che mi sono stati presentati da amici e collaboratori. Alcuni, mediante considerazioni trigonometriche, equazioni delle circonferenze e relative condizioni di tangenza, hanno risolto il problema trovando R = 2 e r = 1 e verificando empiricamente che i triangoli “rossi” sono rettangoli. Una soluzione brillante, che utilizza il Teorema di Descartes, è quella proposta da Daniel Malesani che riporto di seguito.
“… una possibilità per risolvere l’esercizio è usare il teorema di Cartesio delle 4 circonferenze (https://it.wikipedia.org/wiki/Teorema_di_Descartes). In questo modo, si ragiona al contrario: prima si determina il raggio della circonferenza più piccola e poi (volendo) si può dimostrare che il triangolo in questione è rettangolo.
Indichiamo con r il raggio del cerchio più piccolo ed R il raggio del semicerchio più piccolo.
Per cominciare, determiniamo R. Con riferimento alla figura, consideriamo il triangolo rettangolo ADE. Si ha:
AD = AC/2 = 3,
AE = AB – BE = 6-R,
DE = DH + HE = 3+R;
quindi, per il teorema di Pitagora:
DE² = AD² + AE² ⇒ (3+R)² = 3² + (6-R)² ⇒ R = 2.
Ora tiriamo in ballo il teorema di Descartes, che lega le curvature (cioè i reciproci, con segno, dei raggi) delle 4 circonferenze:
(-1/6 + 1/3 + 1/2 + 1/r)² = 2(1/6² + 1/3² + 1/2² + 1/r²).
Questa equazione ha due soluzioni: r = 1 ed r = 3. Entrambe le soluzioni sono geometricamente possibili, ma r = 1 è quella che ci interessa (r = 3 corrisponde ad un cerchio che sta al di sotto della figura, tangente in A al segmento AB).
Credo che questo concluda la soluzione del problema. Andando a ritroso, se si vuole, si può anche verificare che il triangolo DFE è rettangolo, infatti:
EF = EJ + JF = 3;
DF = DK + KF = 4;
DE = DH + HE = 5.
Questi 3 numeri formano l’arcinota terna pitagorica, per cui il triangolo DFE è rettangolo.”
Perché nella soluzione di (2) si dà per scontato che i sue triangoli “rossi” siano rettangoli: ho già scritto che mi sfugge questo forse piccolo particolare…