Menu
I Giochi del Lunedì di Prisma del 13 febbraio 2023 a cura di Fabio Ciuffoli
Ieri abbiamo presentato tre problemi di geometria tratti dal sito web di matematica ricreativa Dare2Solve. Di seguito presentiamo le soluzioni.
Osare la soluzione! – soluzioni
1. Dal vertice in basso a sinistra del quadrato, vengono tracciati due segmenti inclinati dello steso angolo α, che intersecano due lati del quadrato nei punti indicati a distanza rispettivamente di 4 e 6. Calcolare l’area blu compresa tra i due segmenti e i lati del quadrato.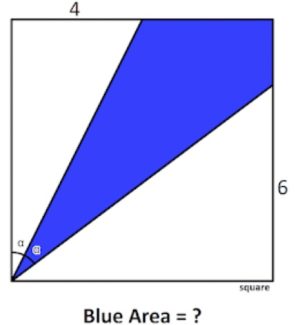
1. SOLUZIONE. Il triangolo con due lati rossi è isoscele, poiché ha due angoli, 90 – α, uguali e quindi i lati obliqui misurano 10. Ora con Pitagora calcoliamo il lato del quadrato: √ (102 – 62) = 8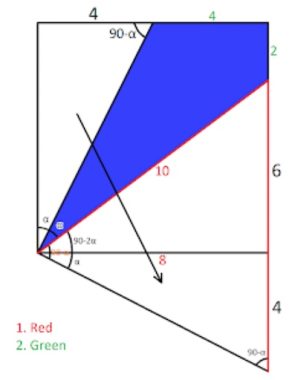
A questo punto calcoliamo l’area del quadrato dalla quale sottriamo le aree dei due triangoli bianchi interni e così troveremo area blu: 64 – (4*8/2 + 6*8/2) = 24u2.
2. Calcolare l’area blu.
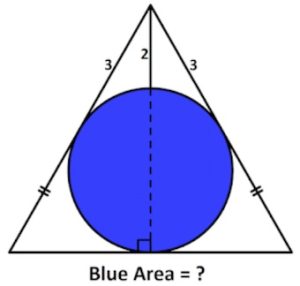
2. SOLUZIONE. Si tratta di un cerchio inscritto in un triangolo equilatero.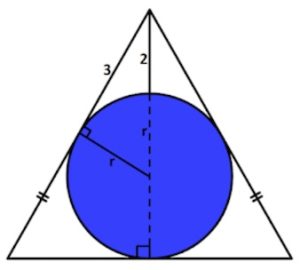 
Applichiamo Pitagora al triangolo rettangolo di cateti 3 e r e di ipotenusa (2 + r) e avremo:
32 + r2 = (2 + r)2 svolgendo 9 + r2 = 4 + r2 + 4r e infine r = 5/4.
Area blu πr2 = 25/16π.
3. Calcolare l’area blu.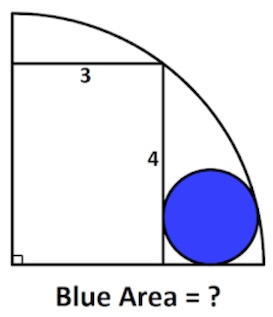
3. SOLUZIONE. Con Pitagora calcoliamo il raggio R del quarto di cerchio R = √ (32 + 42) = 5.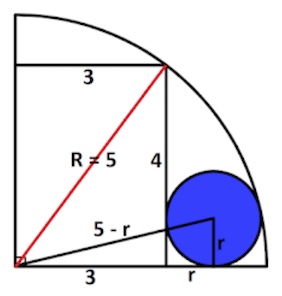 
Ora, definendo r il raggio del cerchio piccolo, nuovamente con Pitagora calcoliamo r. Avremo (5 – r)2 = r2 + (3 + r)2 svolgendo 25 + r2 – 10r = r2 + 9 + r2 + 6r che diviene r2 + 16r – 16 = 0.
La soluzione accettabile dell’equazione di secondo grado è r ≈ 0,94.
L’area blu è quindi 3,14 * 0,942 ≈ 2,77 u2.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
4 risposte
Il triangolo è isoscele. Posso calcolare metà della base (quindi il segmento per intero) col teorema di Pitagora. Calcolo poi l’area con la nota formula. Posso quindi calcolare il perimetro e applicare la formula: 2 area/perimetro = raggio circonferenza inscritta.
Infine, Area cerchio =r•r•π.
Interessanti e stimolanti. Il secondo problema lo si può risolvere anche adoperando il teorema della secante e della tangente: il risultato è immediato. Il triangolo nella fattispecie, però, non è equilatero, perché l’altezza relativa alla base è un numero razionale ( 2+ 5/2) e se fosse equilatero, avremmo una contraddizione rispetto al fatto che il lato dovrebbe misurare 6u, avendo così lato e altezza entrambi razionali.
Bellissima la soluzione 1.
Davvero semplice ed elegante!
Per il problema 2, Fabio dici che si tratta di un triangolo equilatero.
Sicuro che il procedimento non si applichi anche al caso più generico di triangolo isoscele?
Ottima osservazione, il procedimento si può applicare anche ai triangoli isosceli. Non correggo il testo della soluzione per dare valore a questo scambio di opinioni.