80. Soluzioni del 6 febbraio 2023 – Pillole matematiche

Le soluzioni del 6 febbraio 2023 a cura di Fabio Ciuffoli

Ieri abbiamo presentato tre problemi tratti dal libro Pillole Matematiche di Piergiorgio Odifreddi e di seguito pubblichiamo le nostre proposte di soluzione. 

Pillole matematiche – soluzione

1. Meandri fluviali. In condizioni ottimali il percorso di un fiume, in determinate aree, tende a formare meandri. I meandri possono considerarsi una successione di semicirconferenze, di diametro variabile, disposte ordinatamente sul segmento che unisce in linea d’aria l’inizio e la fine, come schematizzato in figura a lato. 

In questa condizione ideale, ipotizzando che la distanza tra A e B sia di 100 chilometri, come è possibile calcolare la lunghezza del fiume?

1. SOLUZIONE. Poiché ogni semicirconferenza ha una lunghezza pari al suo raggio per π, la somma delle lunghezze delle varie semicirconferenze, che corrisponde alla lunghezza del fiume, sarà pari a π moltiplicato per la somma dei vari raggi, che corrispondono alla metà della distanza tra A e B.

Nel nostro caso: π (100/2) = 157 chilometri.

2. Il problema della Jeep. Un esploratore vuole attraversare il deserto con la sua Jeep. L’auto può trasportare al massimo il carburante sufficiente per attraversare metà deserto e esiste un solo distributore di carburante che si trova nella località di partenza.
Come può attraversare il deserto? E quanti carichi di carburante dovrà consumare per portare a termine l’impresa?

2. SOLUZIONE. In sintesi il problema chiede come si possa attraversare un deserto di lunghezza 2 con una Jeep che può trasportare al massimo il carburante necessario per percorrere la distanza 1.
 Dividiamo il tragitto in due parti di lunghezza 1 e dividiamo la prima parte in ulteriori piccole parti, come schematizzato in figura seguente (non in scala). 

Partiamo dal punto H e procediamo a ritroso.

• 1) L’obiettivo è avere 1 pieno in H posto a distanza 1 dall’origine.
• 2) Per avere 1 pieno in H, occorre avere 2 pieni in G posto a 1/3 di distanza da H.
Infatti, parto da G con un pieno, percorro GH consumando 1/3, deposito 1/3 in H, percorro HG consumando il rimanente 1/3. Ora per il secondo viaggio carico il secondo pieno in G, percorro GH consumando 1/3 e mi ritrovo in H con 2/3 nel serbatoio più 1/3 depositato prima.
• 3) Per avere 2 pieni in G, occorre avere 3 pieni in F, posto a 1/5 da G. Infatti parto da F con un pieno percorro FG consumando 1/5, deposito 3/5 in G, percorro GF consumando il rimanente 1/5. Al secondo viaggio incremento il deposito in G di altri 3/5 e al terzo viaggio, arrivo in G con 4/5 di serbatoio che sommati ai 6/5 in deposito mi danno 2 pieni.
• 4) Per avere 3 pieni in F, occorre avere 4 pieni in E, posto a 1/7 da F.
 Sono necessari 4 partenza da E per depositare in F (5/7 + 5/7 + 5/7) e avere 6/7 in serbatoio per un totale di 21/7 cioè 3 pieni.
• 5) Per avere 4 pieni in E, occorre avere 5 pieni in D, posto a 1/9 da E e così via.

Procediamo allo stesso modo, all’ottavo passaggio ci si trova addirittura un po’ prima dell’origine, quindi facendo 8 pieni di carburante nel punto A si riesce ad attraversare il deserto. Infatti: 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/13 + 1/15 = 1,02180042…

In generale, posta uguale ad 1 la distanza che si percorre con un pieno, si possono trasportare n pieni in un punto X se si hanno (n+1) pieni in un altro punto che dista 1/(2n+1) da X.

Estremizzando, non ci sono limiti alla distanza che si può percorrere avendo a disposizione un carburante illimitato, anche se in ogni viaggio la jeep ne può trasportare solo una quantità limitata. 

3. Il giro del mondo in aereo. 
Un aereo deve compiere il giro della Terra senza scalo, ma può trasportare carburante sufficiente solo per metà del viaggio. Altri aerei dello stesso tipo possono raggiungerlo e rifornirlo in volo ma devono ritornare alla base.
 Come può essere organizzata l’impresa?

3. SOLUZIONE. Tre aerei sono sufficienti ad assicurare il volo di un aereo attorno alla Terra. Vi sono molti modi per realizzare il giro, ma il seguente sembra il più efficace perché si usano solo cinque serbatoi di carburante e presenta una certa simmetria di sviluppo.

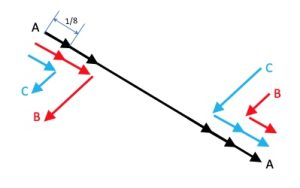
Gli aerei A, B e C partono insieme. Dopo aver percorso 1/8 della distanza totale, C trasferisce 1/4 del suo carburante ad A e 1/4 a B, perciò C resta con 1/4 di serbatoio che è sufficiente per tornare al punto di partenza. A e B continuano insieme ancora per 1/8 di percorso, poi B trasferisce 1/4 di serbatoio ad A perciò B rimane con 1/2 serbatoio, proprio quanto gli basta per tornare indietro alla base, dove arriverà col serbatoio vuoto.

L’aereo A, col serbatoio pieno, continua il volo sino ad 1/4 di distanza dalla base di arrivo dove  resterebbe senza carburante. Qui viene incontrato da C, che si è rifornito alla base e che gli trasferisce 1/4 di carburante, dopodiché entrambi si dirigono alla base. I due aerei resterebbero senza carburante a una distanza di 1/8 di percorso dalla base. A questo punto vengono incontrati dall’aereo B che ha fatto rifornimento per cui B trasferisce ad ognuno degli altri due 1/4 del suo serbatoio e tutti e tre gli aerei hanno ora esattamente il carburante sufficiente per raggiungere la base, sani e salvi.

A lunedì prossimo.