
I Giochi del Lunedì di Prisma del 14 novembre 2022 a cura di Fabio Ciuffoli
Oggi presentiamo quattro problemi di geometria proposti da Catriona Shearer, insegnante e appassionata divulgatrice di matematica. Invitiamo i lettori a inviarci osservazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le soluzioni.
La geometria a colori di Catriona
1. I quattro triangoli colorati sono equilateri. Quale rapporto c’è tra l’area dei triangoli colorati e l’area del rettangolo?
2. I tre rettangoli sovrapposti sono congruenti, ciascuno di area 4. I punti neri segnano i punti medi dei lati corti. Qual è l’area totale del disegno?
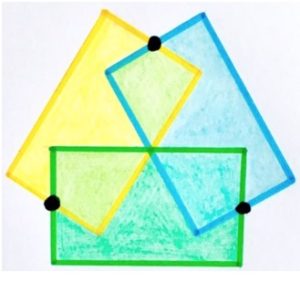
3. Due cerchi e due quadrati. Determinare l’area del quadrato piccolo.
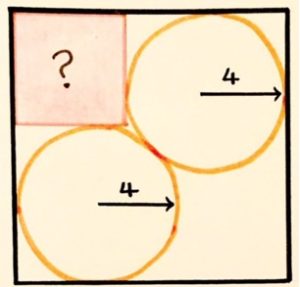
4. Quattro triangoli equilateri sono stati disegnati sui lati di un quadrato di area 12. Quanto misura l’area ombreggiata color celeste?
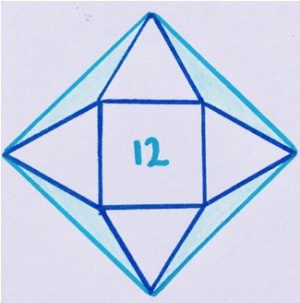
Aggiornamento per le soluzioni click qui
I giochi di oggi sono tratti dall’account twitter di Catriona Shearer https://mobile.twitter.com/Cshearer41
Questa è la seconda puntata che il nostro blog dedica a Catriona. La prima puntata si trova al link https://www.prismamagazine.it/giochi/10-giochi-del-13-settembre-2021-gli-enigmi-colorati-di-catriona/
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
19 risposte
4. Vedi allegato
Problema 4
Area del quadrato centrale AQc=12
Lato LQc= radq(12) = 3,464102
Lato dei triangoli = LQc = 3,464102
Area dei triangoli = ATr = (radq(3)/4)*LQc^2 = 5,1961
Altezza triangoli hT = (LQc*radq(3))/2 = 3
Diagonale quadrato maggiore diagQ =9,464102
Lato quadrato maggiore = diagQ/radq(2) = 6,69213
Area quadrato maggiore = AQm = 44,78461
Area poligoni interni AP= AQc + 4*ATr = 32,78461
Area vuota = AQm – AP = 12
Perfetto.
2. vedi allegato
Dette a e b le misure dei lati di ciascun rettangolo, la sovrapposizione dei rettangoli giallo/azzurro, verde/azzurro e verde/giallo danno luogo ciascuno ad un quadrilatero somma di due triangoli rettangoli con cateti a/2 e b/2 e quindi ciascuno con superficie:
2•(1/2)•(a/2)•(b/2)=ab/4
La superficie richiesta vale pertanto:
3•ab-3•ab/4=(9/4)ab=(9/4)•4=9
Allora l’area ombreggiata un quadrato
Troviamo il suo lato c. L’area 12 e un c è uguale a √(12)
Dunque i lati dei triangoli b = √12
I triangoli sono equilateri, allora l’altezza h passa per metà della base b dividendola in due, così avremo un triangolo rettangolo di lati b = √12 , b/2= √12)/2
Applichiamo Pitagora h^2=((√(12))/2)^2 + √12^2
h^2. =12/4+12
=3+12 =15
h. =√15
D =2√15+√12
2c^2 = (2√15+√12)^2
c=. (2√15+√12)/√2
A =c^2 =(2√15+√12)^2/2
C’è qualche errore nei calcoli.
1. 2/3 vedi immagine allegata
Quesito 4. Lato triangolo = 4, altezza 2sqrt(3)
Diagonale quadrato grande: 4(1+sqrt(3))
Area= 8(1+sqrt(3))^2 – 12-4*4sqrt(3) = 24 + 16sqrt(3) – 12 – 16sqrt(3) = 12
Quesito 1 Per lato base = 1, l’area dei triangoli è = RADQ(3)/4 + 2*RADQ(3)/6 + RADQ(36) = (4/9)RADQ(3)
L’area del rettangolo è = (2/3)RADQ(3)
Quindi il rapporto tra l’area dei triangoli colorati e l’area del rettangolo in cui sono contenuti è 2/3
Buongiorno.✅ Problema n°2 ⇒Area totale=9 u²✅. Problema n°3 ⇒. Area▢piccolo=[4•√2•(1+√2)–8]²=32 u²✅.
N. 2. Il risultato è 9. Vedi immagine allegato
1) 29/36
A domani per le soluzioni
Ci provo.
Quesito 1: Il rapporto è 1 su radice 3
Quesito 2: L’area del disegno è 9
Quesito 3: L’area è 32
Quesito 4: L’area ombreggiata è 12
Perfetto.
Questa mattina ho semplificato troppo il quesito 1. Ho fatto i conti usando 4 triangoli equilateri uguali all’interno di un quadrato pensando mantenesse lo stesso rapporto rispetto ad un generico rettangolo. Invece noto che con un rettangolo il rapporto tra le aree diventa 2/3 al posto di 1 su radice 3.
Al problema 3. 32? Ma sono appena sveglio…
Problema n 3.
La diagonale del quadrato grande è 8 + 8sqrt(2), pertanto il lato di questo quadrato è 4sqrt(2) + 8. Ne segue che il lato del quadrato piccolo è pari a 4sqrt(2) (lo si ottiene dal lato di quello grande meno il diametro della circonferenza) e la sua area risulta 32