
Soluzioni del 31 ottobre 2022 a cura di Fabio Ciuffoli
Ieri abbiamo proposto due giochi utilizzando alcuni simboli antichi e ricchi di significato: Yin Yang e pentagono regolare. Pubblichiamo di seguito le soluzioni che offrono più di uno spunto per mettere in relazione matematica, armonia e bellezza.
É la matematica armonia e bellezza! – soluzioni
1. Yin Yang. Rappresentiamo il simbolo Yin-Yang in una circonferenza di diametro 2. La distanza tra i due centri dei cerchietti piccoli è uguale a 1. Calcolare la lunghezza del segmento arancione e del segmento blu.
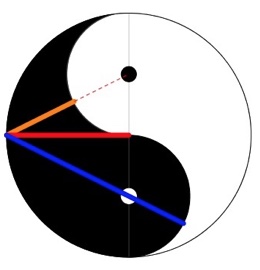
1. SOLUZIONE. Con Pitagora si calcola:
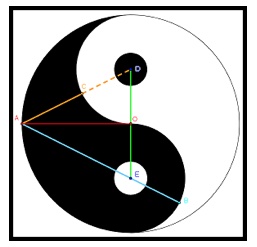 In un altro modo si può calcolare la distanza tra il punto A e i punti D e E che è √ [(12 + (1/2)2] = (√ 5)/2 e poi si determina:
In un altro modo si può calcolare la distanza tra il punto A e i punti D e E che è √ [(12 + (1/2)2] = (√ 5)/2 e poi si determina:
Avete notato, la misura del segmento blu è il numero aureo φ e quella del segmento arancione è 1/ φ. Il numero aureo è considerato sintesi di bellezza, grazia e divina proporzione. Infatti, a buona ragione, nel simbolo Yin Yang c’è bellezza, equilibrio, grazia e armonia.
John Arioni ha pubblicato, sulla pagina facebook di Cut The Knot Math del compianto Alexander Bogomolny, la seguente immagine nella quale viene evidenziata un’ulteriore sezione aurea.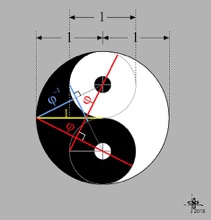
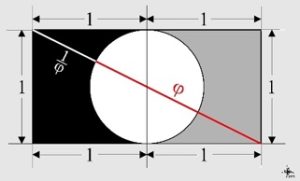
John ha dichiarato di essere stato portato a trovare la sezione aurea in Yin-Yang da una sua precedente scoperta su due quadrati e un cerchio disposti come in figura seguente. Le immagini valgono più di ogni descrizione.
2. Pentagono regolare. In figura è disegnato un pentagono regolare di lato 1. Siete in grado di determinare il rapporto tra la diagonale AD e il lato AB?
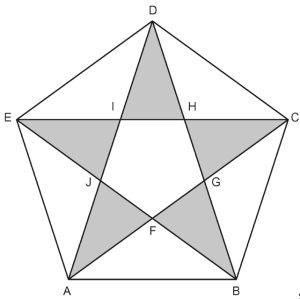 2. SOLUZIONE. Ci sono diversi metodi per la dimostrazione, alcuni abbastanza semplici e altri più complessi. Esaminiamo il triangolo ADB, uno dei tre triangoli isosceli che appaiono in figura. I suoi lati uguali AD = BD sono anche la misura della diagonale del pentagono, che equivale al lato della stella pentagonale. Il lato AB sappiamo che misura 1. Osservando BJ, che è la bisettrice dell’angolo DBA, si può vedere che il triangolo BJA ha gli stessi angoli del triangolo iniziale ADB e perciò sono simili. Quindi si può verificare AD : AB = AB : AJ.
2. SOLUZIONE. Ci sono diversi metodi per la dimostrazione, alcuni abbastanza semplici e altri più complessi. Esaminiamo il triangolo ADB, uno dei tre triangoli isosceli che appaiono in figura. I suoi lati uguali AD = BD sono anche la misura della diagonale del pentagono, che equivale al lato della stella pentagonale. Il lato AB sappiamo che misura 1. Osservando BJ, che è la bisettrice dell’angolo DBA, si può vedere che il triangolo BJA ha gli stessi angoli del triangolo iniziale ADB e perciò sono simili. Quindi si può verificare AD : AB = AB : AJ.
Dato che AB = JB = JD = 1 e AJ = AD – 1. Ora, sostituendo nella precedente, abbiamo AD : 1 = 1 : (AD – 1).
Svolgendo AD (AD – 1) = 1 che diviene AD² – AD – 1 = 0. La soluzione positiva dell’equazione di secondo grado è AD = [(√5)+ 1] / 2 = 1,618, quindi il rapporto tra la diagonale AD e il lato AB è 1,618. Compare di nuovo il numero aureo φ, un’ulteriore conferma del pentagono e della stella come forme di bellezza, equilibrio, grazia e armonia.
Per chi volesse approfondire. Il triangolo ADB è un triangolo aureo, ossia con i due lati uguali in rapporto aureo con il terzo lato (≈ 1,618) e angoli di 36°, 72° e 72°. Per ulteriori approfondimenti https://it.wikipedia.org/wiki/Triangolo_aureo
A lunedì prossimo
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).