61. Soluzioni del 19 settembre 2022 – Spunti matematici dall’India

Le soluzioni del 19 settembre 2022 a cura di Fabio Ciuffoli

Ieri abbiamo proposto quattro giochi logici tratti dall’interessante sito indiano di divulgazione matematica Cuemath e di seguito presentiamo le soluzioni. 

Spunti matematici dall’India – soluzioni 

Roberto, Giulio e Mario lavorano in un negozio di cartoleria che vende penne, gomme e matite.

• Roberto dice: “Sette penne e cinque gomme costano come sei matite”.
• Giulio dice: “Quattro penne e nove matite costano come cinque gomme”.
• Mario dice: “Sei matite e tre gomme costano come quattro penne”.

Solo uno sta mentendo. Sapreste individuare chi?

1. SOLUZIONE. Sia P il prezzo delle penne, G il prezzo delle gomme e M il prezzo delle matite.Roberto sta dicendo che 7P + 5G = 6M. Giulio sta dicendo che 4P + 9M = 5G. Mario sta dicendo che 6M + 3G = 4P. Combinando le affermazioni di Roberto e Giulio, otteniamo 11P = – 3M. Questo è impossibile. Combinando le affermazioni di Giulio e Mario, otteniamo 15M = 2G. Questo è possibile. Combinando le affermazioni di Mario e Roberto, otteniamo 8G = – 3P. Questo è impossibile. A questo punto: o Roberto sta mentendo, che significa che Giulio e Mario stanno dicendo la verità e questo è compatibile con le combinazioni delle affermazioni; oppure Roberto dice il vero e ciò significa che Giulio deve mentire (dal momento che se anche Giulio stesse dicendo la verità, la combinazione delle affermazioni di Roberto e Giulio non sarebbe impossibile) e anche Mario deve mentire (per gli stessi motivi). Ma poiché può esserci un solo bugiardo, possiamo eliminare questa seconda ipotesi e quindi Roberto è il bugiardo.

2. L’insegnante è tornato in classe e ha visto un vaso di fiori rotto. Ha interrogato 4 studenti, che hanno risposto così:

• Aldo: “Non è stato Bruno. E’ stato Daniele”.
• Bruno: “Non è stato Carlo. Non è stato Daniele”.
• Carlo: “Non è stato Daniele. E’ stato Bruno”.
• Daniele: “E’ stato Carlo. E’ stato Bruno”.

È noto che nelle risposte di ciascuno studente c’è una dichiarazione vera e una falsa. Chi ha rotto il vaso?

2. SOLUZIONE. Una delle affermazioni di Bruno è falsa, quindi il colpevole deve essere Carlo o Daniele e poiché una delle affermazioni di Daniele è vera, il colpevole deve essere Carlo o Bruno. Incrociando le due ipotesi si deduce che Carlo è il colpevole. Aldo e Carlo forniscono due risposte logicamente identiche, ciascuna con una dichiarazione vera (“Non è stato Bruno”) e una falsa (“E’ stato Daniele”) e sono entrambe compatibili con l’ipotesi di Carlo colpevole. Una procedura alternativa, più analitica ma anche più lunga, consiste nell’analizzare le quattro ipotesi di colpevolezza e verificare la verità o falsità delle affermazioni di ciascuno studente.  In tabella sono riportate le quattro ipotesi e i valori di vero o falso per ciascuna risposta.  In rosso sono evidenziate le contraddizioni.

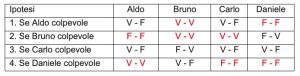
L’unica ipotesi senza contraddizioni è Carlo colpevole.

3. L’inevitabile gioco logico sui cappelli. Un gruppo di persone è in una stanza e tutti indossano un cappello arancione o blu. Ogni persona può vedere il cappello delle altre persone ma non il proprio. Uno di loro dice: “Se riesci a vedere almeno 6 cappelli arancioni e almeno 6 cappelli blu, alza il braccio!”. Esattamente 12 persone alzano il braccio. Quante persone ci sono nella stanza?

3. SOLUZIONE. Ipotizziamo che ci siano almeno 6 persone con cappelli arancioni e 6 persone con cappelli blu e poiché nessuno può vedere il proprio cappello, nessuno alzerebbe il braccio, quindi devono esserci più persone. Se ci fossero più di 7 persone con un cappello arancione e più di 7 persone con un cappello blu, allora ci sarebbero più di 14 persone che alzerebbero il braccio, più delle 12 effettive. Pertanto devono esserci 6 persone con un cappello di un colore (diciamo, arancione) e più di 6 con un cappello dell’altro colore (blu). Le persone con un cappello arancione possono vedere solo altri 5 cappelli arancioni, quindi non alzano il braccio. Ma tutte le persone con un cappello blu alzeranno il braccio. Quindi ci sono 12 persone con i cappelli blu. Ora, aggiungendo 6 con il cappello arancione, otteniamo un totale di 18. Le persone nella stanza sono 18.

4. Quattro persone A, B, C e D sono coinvolte in un crimine e sono stati accertati i seguenti fatti:

• (1) Se entrambi A e B sono colpevoli, allora C è stato complice.
• (2) Se A è colpevole, allora almeno uno tra B e C è stato complice.
• (3) Se C è colpevole, allora D è stato complice.
• (4) Se A è innocente allora D è colpevole.

Quali sono sicuramente i colpevoli?

4. SOLUZIONE. Ipotizziamo che A sia colpevole. Per (2) o B o C sono colpevoli. Se B è innocente, allora C deve essere colpevole. Ma supponiamo che B sia colpevole. Allora A e B sono entrambi colpevoli, quindi per (1) C è colpevole. Ciò dimostra che se A è colpevole, lo è anche C. Inoltre, da (3) se C è colpevole, lo è anche D. Combinando questi due fatti, deduciamo che se A è colpevole, lo è anche D. Ora ipotizziamo che A sia innocente, allora per (4) D è colpevole. Pertanto, indipendentemente dal fatto che A sia colpevole o innocente, D è colpevole. Così D è sicuramente colpevole, tutto il resto è dubbio.

A lunedì prossimo.