
I giochi del lunedì di Prisma 16 agosto 2021 a cura di Fabio Ciuffoli
Presentiamo due problemi di strategia, sotto forma di giochi e invitiamo i lettori a comunicarci osservazioni e proposte di soluzione nello spazio dei commenti. Alle ore 17.00 di domani pubblicheremo le soluzioni.
Pizza gratis con la matematica
1. Vai a mangiare una pizza con un tuo amico o collega. Gli dici di tagliare la pizza in quante fette vuole, purché siano pari, affinché possiate mangiarne lo stesso numero. Possono essere grandi, piccole, alcune grandi e altre piccole, possono essere due, quattro, venti o più. 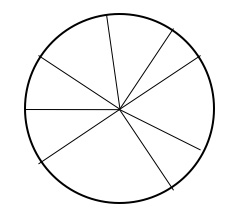
Ora cominciate a mangiare la pizza, scegliendo a turno le fette con due sole regole: 1. siccome il tuo amico ha diviso la pizza come ha voluto, ora toccherà a te scegliere per primo; 2. si possono scegliere solo fette vicino alla parte vuota, quella della pizza che è già stata mangiata, quindi non si possono prendere fette in qualunque punto della pizza. A eccezione della prima fetta, che può essere qualunque dato che ancora non c’è un vuoto.
Se il tuo amico riesce a mangiare più pizza di te, paghi tu la pizza. Se tu mangi più pizza oppure se mangiate la stessa quantità, paga lui. Sapresti indicare chi dei due ha una strategia vincente e quale?
2. Monete gratis con la matematica. Dici a un tuo amico di disporre in linea un numero pari di monete. Possono essere quante vuole, del valore che vuole e nell’ordine che desidera. Il gioco consiste nel prelevare a turno una delle monete che stanno all’estremità della fila. Siccome lui ha disposto le monete, spetta a te la prima scelta.
Se il tuo amico riesce ad accumulare una somma di denaro più grande della tua, se lo prende tutto. Se tu riesci a mettere insieme la stessa somma o una somma maggiore della sua, allora vinci e il denaro è tuo. Qual è la tua strategia vincente?
Aggiornamento: per le soluzioni click qui
I giochi di oggi sono rielaborazioni tratte dal libro Intelligenza matematica di E. S. de Cabezon.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
12 risposte
E’ molto semplice Partiamo dal secondo problema
Sommiamo il valore delle monete di posto pari e separatamente quelle di posto dispari
Dal confronto si sa quale delle due sequenze produce la somma maggiore
A questo punto il primo sceglierà sempre le monete di quella stessa parità
Es. 1, 50c, 1c, 50c, 10c, 20c
Abbiamo 1,11 di posto dispari contro 1,20 di posto pari
Il primo quindi non prenderà 1 ma 20c
Il secondo dovrà scegliere tra 1 e 10c
Se il secondo prende 1, il primo prenderà il 50c sinistro, se il secondo prende 10c il primo prenderà il 50c destro
…
Alla fine il primo collezionerà 1,20 l’altro 1,11
—-
A questo punto è chiara la strategia anche per il primo problema
Sommare le fette di posto pari tra loro e quelle di posto dispari tra loro
Non resta al primo che partire da una fetta la cui parità ha alla maggior resa
e scegliere sempre la fetta disponibile di quella parità
Chiarissimo. Domanda aggiuntiva. E se cadesse il vincolo del numero pari di monete o di fette di pizza e il secondo giocatore potesse scegliere se pari o dispari, cosa cambierebbe?
Il secondo dopo la scelta del primo avrà un numero pari di monete davanti per cui utilizzerà il criterio precedente con questa modifica
Sommerà i valori di posto pari e di posto dispari separatamente
Aggiungerà il valore della moneta scelta dal primo alla sequenza pari confrontandola con quella dispari e poi alla sequenza dispari confrontandola con quella pari
Questo non garantirà al secondo di vincere perché entrambe le eventualità potrebbero essere perdenti ma laddove ci fosse un vantaggio deve seguire quella sequenza
Es. 20c, 10c, 1, 50c, 5c
Se il primo sceglie 20c abbiamo 60c contro 1,05 residui
Poiché 1,05>20c+60c il secondo sceglierà la sequenza 5c+1
Se invece il primo sceglie 5c abbiamo 1,20 contro 60c residui
Poiché 1,20>60c+5c il secondo sceglierà la sequenza 20c+1
Ottima analisi, valida anche nel caso di una disposizione di monete randomizzata. Nel nostro problema, la disposizione non è casuale ma è a cura del secondo giocatore che dovrà tener conto della differenza da te segnalata, ad esempio mettendo monete di valore molto basso ai due lati. Quindi il secondo giocatore avrà sempre una strategia vincente, anche se il primo prenderà più monete.
Ho provsto con alcune simulazioni a risolverr il problema due. Con 2 monete vince fscilmente il primo giocatore; con 4 monete le permutazioni possibili sono 24 e mi risulta difficile capire chi potrebbe vincere. Addirittura se le monete fossero 6, le permutazioni possibili sarebbero.720. Troppo complicato. Attendo soluzione.
Effettivamente la via analitica, proposta da Davide, è molto complicata, ma ha il pregio di farci capire le numerosissime combinazioni o permutazioni che può utilizzare il secondo giocatore. Nonostante questo, il primo giocatore ha sempre una strategia vincente.
Inizio a riflettere, ma non ho la soluzione. Le fette non devono essere tutte uguali e devono essere almeno sei affinché chi taglia possa vincere. Con 2 fette o quattro vince sempre chi sceglie per primo.
Chi taglia potrebbe mettere due grandi di dimensioni diverse vicine e poi alternate una piccola e una grande in modo tale che chi sceglie per primo possa scegliere una grande solo all’inizio. Non riesco a generalizzare una strategia di vittoria per chi sceglie per primo indipendente dal taglio.
Il problema delle monete, per similitudine, può essere d’aiuto per la soluzione del problema della pizza. Ovviamente, come hai detto, con due monete vince sempre chi sceglie per primo, anche con con quattro, ma anche con 6 o 8 o 10 ecc. Il primo dovrà scegliere dopo aver contato i valori delle monete in posizione pari o dispari e poi decidere da qual iniziare … a domani per le soluzioni complete.
Pizza: penso che vinca sempre chi prende per primo. Se le fette sono tutte uguali e di numero pari finisce alla pari e vince il primo; se sono uguali e in numero dispari vince chi prende per primo; se sono di dimensioni diverse, partendo dalla più grande il primo dovrebbe restare sempre in vantaggio.
Ovviamente il nostro amico, che taglia la pizza o dispone le monete, lo farà nel modo in cui possa vincere quindi taglierà e disporrà nel modo a lui più conveniente. Il primo a scegliere ha sempre una strategia vincente, ma non sempre è vero che se sceglie la più grande (pizza o moneta) vince.
Non è sempre così! Mi sembra di aver capito che tu dici di prendere inizialmente la più grande e continuare con questa strategia. Ad esempio se il tuo amico disponesse le monete in questa sequenza: 1 – 2 – 0,5 – 0,1 allora tu prenderesti 1, lui 2 poi tu ancora prenderesti 0,5 e infine lui prenderebbe 0,1. Vince lui con 2,1 contro 1,5!?!
1. Toccando a me scegliere per primo, posso prendere la fetta più grossa. Il mio amico dovrà prendere una delle due fette intorno, che sono piccole. Andando avanti così, sia se il mio amico prende a destra che se prende a sinistra, mangerò sempre più pizza io, se scelgo, tra le due fette intorno, la più grande.
2. Tu prendi la moneta più grande delle due che sono a “capofila” (o, se sono di pari valore, quella accanto ad una piccola). Continuando sempre con questa strategia, è sicuro vincere. Anche perché, siccome all’amico tocca l’ultima scelta, potrai prendere quella più grande tra le due rimaste.