
Le soluzioni del 4 luglio 2022 a cura di Fabio Ciuffoli
Ieri abbiamo presentato tre problemi sul mondo del ciclismo e di seguito pubblichiamo le soluzioni.
La Grande Boucle – soluzioni
1. Il Re della Montagna sale su un colle a 15 km orari e lo scende a 45 km orari, impiegando due ore. Supponendo che la distanza percorsa in salita e in discesa sia la stessa, quanti kilometri ha percorso in totale?
1. SOLUZIONE. La velocità è data dal rapporto tra distanza e tempo. Durante la salita, quindi 15 = d/t, dove d è la distanza in salita e t è il tempo impiegato per salire. Durante la discesa, 45 = d/T, dove T è il tempo impiegato per scendere. Svolgendo per d, si ottiene d = 15t e d = 45T, quindi 15t = 45T e infine t = 3T, ossia il tempo di salita è tre volte maggiore del tempo di discesa.
Sappiamo che t + T = 2 ore, che diventa 3T + T = 2, da cui T = 1/2. La distanza in discesa è quindi 45/2 = 22,5 km e la distanza totale è 22,5 * 2 = 45 km.
2. Paul e Philippe devono fare un viaggio di 20 km, partendo insieme e arrivando a destinazione nello stesso momento. Hanno una sola bicicletta, che utilizzano a turno. Ogni volta che uno di loro scende dalla bicicletta la lascia sul ciglio della strada e continua a camminare, mentre l’altro, quando raggiunge la bicicletta, la può utilizzare. Paul cammina a 4 km/h e pedala a 10 km/h, mentre Philippe cammina a 5 km/h e pedala a 8 km/h. Supponendo che entrambi stiano camminando o andando in bicicletta e non si fermino mai per riposarsi, come possono organizzare il loro viaggio?
Domanda di approfondimento: A Paul e Philippe si aggiunge Pierre, che cammina a 3 km/h ma pedala a 12 km/h. Come possono organizzare il viaggio, in modo da partire insieme e arrivare insieme?
2. SOLUZIONE. Paul parte in bicicletta e pedala per un’ora, percorrendo 10 km, poi lascia la bicicletta e continua a camminare. Philippe, che cammina a 5km/h, raggiungerà la bicicletta dopo due ore, mentre Paul sarà al km 14. Philippe prende la bicicletta e un’ora dopo sarà al km 18, in coincidenza con l’arrivo di Paul esattamente tre ore dopo la partenza. Tuttavia, il nostro obiettivo è che i due arrivino al km 20 contemporaneamente, non al km 18. Occorre coprire i restanti 2 km in modo da iniziare e arrivare contemporaneamente, quindi devono camminare e pedalare ancora per 2/18 o 1/9 rispetto a quello che hanno già fatto. Quindi Paul riparte in bicicletta per 1/9 d’ora, coprendo 10/9 km e qui dovrà lasciare la bicicletta e poi cammina per 2/9 d’ora. Philippe camminerà per 2/9 d’ora e poi percorrerà in bicicletta il resto. Il viaggio totale è quindi di 3 ore e 3/9 d’ora, ovvero 3 ore e 20 minuti.In questa proposta di soluzione Paul pedala per 10 km, cammina per 8 km, poi pedala per 1 e 1/9 km e cammina per il resto, mentre Philippe percorre a piedi 8 km, poi prende la bicicletta per la prima volta. Questo è un procedimento tra numerosi altri possibili. Il punto chiave è che Paul deve pedalare per primo e la distanza totale da lui percorsa in bicicletta deve essere 11 e 1/9 km. Potrebbe pedalare la sua tratta in una volta sola, se gli piace, o in segmenti più brevi.
Soluzione approfondimento. Nel viaggio Paul deve percorrere 7 e 11/27 km, Philippe per 1 e 13/27 km e Pierre per 11 e 3/27 km.
3. Se si attacca una corda al pedale inferiore e lo si tira indietro, come illustrato dalla freccia rossa, la bicicletta si muove avanti o indietro?
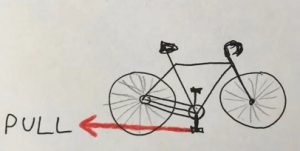
3. SOLUZIONE. La bicicletta si muove all’indietro, mentre il pedale si muove in senso antiorario. O almeno, lo farà in quasi tutte le bici, a parte quelle impostate su una marcia estremamente bassa. È una risposta contro intuitiva e sembra sorprendente anche quando la si prova in pratica. Questo rompicapo ha avuto molto successo qualche anno fa grazie al seguente video del geniale George Hart, dove spiega i meccanismi di ciò che sta accadendo in modo molto chiaro e preciso.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Sul problema n 3 si è sviluppato un bel confronto di opinioni. Riporto di seguito alcuni commenti.
Giovanni Anichini: “Va a destra.”
Franco Capurso: “Avanti verso destra, credo.”
Michele Michele: “Se é messa sul cavalletto va circa 2-5 cm avanti poi cade sulla destra e viene trascinata all indietro.”
Marco Villa: “Va avanti fino a che i pedali non sono orizzontali.”
Gianni Borsano: “Basta fare la prova 😁…tutti abbiamo una bicicletta …e una corda.”
Marco Paperini: “Se la domanda sottintendeva un “senza far strisciare la ruota”, dipende dalla posizione iniziale del pedale: se è verticale, come in figura, va indietro ma striscia fin da subito.”
Ringrazio gli autori per la partecipazione.