50. Soluzioni del 27 giugno 2022 – Quadrati, cerchi e intelligenze matematiche

Le soluzioni del 27 giugno 2022 a cura di Fabio Ciuffoli

Ieri abbiamo presentato un problema sul perimetro e la circonferenza proposto dal Professor Eduardo Saenz de Cabezon, insegnante di Matematica dell’Università la Rioja in Spagna e ore pubblichiamo la soluzione illustrando tre differenti metodi.  

Quadrati, cerchi e intelligenze matematiche – soluzioni

Il professore appese, sul tabellone degli annunci del Dipartimento di Scienze Matematiche, un foglio con il disegno seguente chiedendo di poter vedere la soluzione scritta.

Il problema non è particolarmente difficile, soprattutto per matematici di professione, ma è molto utile per riflettere sui modi di pensare e di affrontare i procedimenti, più o meno complessi, per la soluzione. Le risposte possibili sono tre e solo una è quella corretta: il perimetro è maggiore della circonferenza, la circonferenza è maggiore del perimetro o i due sono uguali. Ma questo non è un test,  facciamo matematica ricreativa e ciò che importa è il ragionamento e il divertimento. Come procedete?

SOLUZIONI. Come accennato, ci sono molteplici modi per approcciare il problema, facendo ricorso alla creatività, al “bagaglio di conoscenze matematiche”, alle tecniche di elaborazione algebrica quali la risoluzione di equazioni, l’uso di seni, coseni, tangenti e le loro relazioni, ecc. Di seguito presentiamo tre metodi, relativamente semplici, per la soluzione.

SOLUZIONE 1. 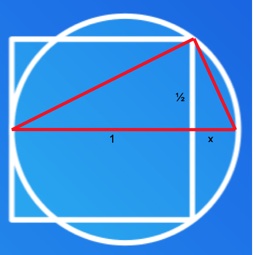Supponiamo che il lato del quadrato misuri 1 e disegniamo un triangolo come in figura. Sappiamo che si tratta di un triangolo rettangolo con base 1 + x e altezza ½.  Sappiamo anche che, applicando Euclide, in ogni triangolo rettangolo l’altezza relativa all’ipotenusa è la media proporzionale tra le proiezioni dei cateti sull’ipotenusa stessa, per cui 1 : ½ = ½ : x. Risolvendo avremo x = ¼. Il diametro della circonferenza è quindi 1 + ¼ = 5/4. Di conseguenza, la circonferenza è 5π/4 = 3,95 e il perimetro del quadrato è 4. Il perimetro è maggiore della circonferenza. La circonferenza e il perimetro avrebbero ugual misura se 5π/4 = 4 ovvero se avessimo un π =16/5 = 3,2 ma ciò è impossibile perché 3,2 è maggiore di π.

SOLUZIONE 2.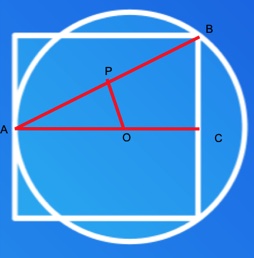
 Prendiamo il punto medio di AB e lo chiamiamo P, ora congiungiamo P con il centro O. Osserviamo che i triangoli ABC e AOP sono simili (in fondo presentiamo la dimostrazione, per ora procediamo).
Essendo AB : OA = AC : AP e AC = 1 e BC = ½ di conseguenza, applicando Pitagora, AB = √ 1 + 1/4  = √ 5/4 = e AP la metà di esso ovvero AP = √ 5/16. Risolvendo la proporzione per OA che è il raggio, abbiamo OA = 5/8. Ora la circonferenza è 2π5/8 che semplificando diviene 5π/4 come nella soluzione precedente. Il perimetro è 4 la circonferenza 5π/4, il perimetro è maggiore della circonferenza.

SOLUZIONE 3. 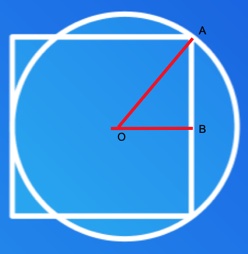Tracciamo la linea OA dal centro della circonferenza a un vertice del quadrato e un’altra OB sempre dal centro della circonferenza fino a metà lato del quadrato. Il triangolo OAB è rettangolo, l’ipotenusa corrisponde al raggio, che chiamiamo R, il cateto AB misura ½ e la lunghezza dell’altro cateto OB che è (1 – R) il lato del quadrato meno in raggio della circonferenza. Con Pitagora avremo: R² = OB² + (1/2)² sostituendo  R² = (1 – R)² + ¼ svolgendo R² = 1 + R² – 2R + ¼. Eliminiamo R² e avremo 2R = 5/4 infine R = 5/8. Come nelle soluzioni precedenti, il perimetro del quadrato 4 è maggiore della circonferenza 5π/4.

Infine, come preannunciato nella soluzione n 2, dimostriamo che i triangoli ABC e AOP sono simili. Il triangolo AOB è isoscele, in quanto i lati OA e OB sono due raggi della circonferenza. Così l’altezza sul lato AB passa per O, essendo ovviamente perpendicolare ad AB attraverso P. Ne consegue che il triangolo APO è rettangolo, come il triangolo ABC. Inoltre condividono l’angolo del vertice in A, quindi hanno due angoli uguali. E se hanno due angoli uguali, ne hanno tre e pertanto sono simili. 

A lunedì prossimo.