45. Soluzioni del 23 maggio 2022 – La scuola di Rachinsky

Soluzioni del 23 maggio 2022 a cura di Fabio Ciuffoli

Ieri mattina abbiamo presentato cinque problemi proposti dal professor Aleksandrovich Rachinsky e ora pubblichiamo le soluzioni. 

La scuola di Rachinsky – soluzioni 

1. Ho comprato 20 kg di zucchero, 5 kg di caffè e 5 kg di tè, e per tutto ho pagato 18 rubli.

• Un chilo di caffè costa quattro volte più di un chilo di zucchero.
• Un chilo di tè è quattro volte più costoso di un chilo di caffè.

Quanto costa un chilo di ciascuno? [Nota: 1 rublo = 100 copechi]

1. SOLUZIONE. Si imposta un sistema di tre equazioni con tre incognite, indicando con z il costo di 1 kg di zucchero, con c il costo di 1 kg di caffè e con t il costo di 1 kg di tè:Lo zucchero costa 15 copechi al kg, il caffè 60 copechi al kg e il tè 2 rubli e 40 copechi al kg.

2.Diversi mendicanti vengono da me. Mi mancano 5 copechi per dare a tutti 7 copechi. Se invece dessi a tutti 6 copechi, allora avrei ancora 10 copechi. Quanti mendicanti vengono e quanti soldi ho?

2. SOLUZIONE. Indichiamo con n il numero di mendicanti e con s la somma a disposizione e impostiamo il seguente sistema:

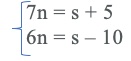
sottraendo membro a membro determiniamo: n = 15, per cui s = 100 copechi.

3. La circonferenza della ruota anteriore di una carrozza è lunga 7 piedi, quella posteriore è lunga 10 piedi. La ruota anteriore ha fatto 150 giri in più dell’altra. Quanto è stato lungo il viaggio in carrozza? [Nota: 1 piede = 30,48 cm, 1 miglio = 5280 piedi]

3. SOLUZIONE. Dopo 70 piedi la ruota anteriore ha compiuto 10 giri mentre la ruota posteriore ne ha compiuti 7, quindi  la ruota anteriore ha compiuto 3 giri in più della posteriore. Se l’anteriore ne ha compiti 150 in più, allora sono stati percorsi 150/3 = 50 * 70 = 3.500 piedi. Un altro metodo di soluzione prevede l’impostazione di un’equazione, indicando con n il numero di giri della ruota posteriore:

10n = 7(n + 150);     che diviene 3n = 1.050      per cui n = 350.      Infine 350 * 10 = 3.500 piedi.

4. Si deve scavare un tunnel attraverso la montagna, lungo 1 versta, largo 8 sazhen e alto 3 sazhen. Quanto tempo impiegano 150 operai a scavarlo, se ognuno scava un sazhen cubico in 2 giorni? [Nota: Il tunnel ha la forma di un parallelepipedo rettangolo; 1 versta = 500 sazhen.]

4. SOLUZIONE. Il volume si può facilmente calcolare a mente: V = 500 * 8 * 3 = 12.000 sahzen cubici. Poiché ogni operaio impiega 2 giorni per scavare un sazhen cubico, basta dividere il volume per 75, ottenendo il numero dei giorni necessari per lo scavo. 12.000/ 75 = 160 giorni.

5. Ho fatto scavare un laghetto lungo 8 sazhen, largo 4 sazhen e profondo 1 sazhen 1 arshin 8 vershok. Per ogni sazhen cubico scavato ho speso 1 rublo e 50 copechi. Quanto ho pagato? [Nota: il laghetto ha la forma di un parallelepipedo rettangolo; 1 sazhen = 3 arshin, 1 arshin = 16 vershok.]

5. SOLUZIONE. Il volume si può calcolare: V = 8 * 4 * (1 +1/3 + 8 * 1/3 *1/16) = 48 arshin cubici.  Moltiplicando il volume per 1,5 si ottiene la spesa:  (48 * 1,5) = 72 rubli.

A lunedì prossimo.