Menu
Le soluzioni del 9 maggio 2022 a cura di Fabio Ciuffoli
Ieri abbiamo proposto due problemi provenienti dal mondo della scuola e ora presentiamo le soluzioni.
Prove d’esame – soluzioni
1. Il cerchio di raggio R centrato nel vertice in basso a sinistra del quadrato in figura ne ricopre metà della superficie; il cerchio di raggio r centrato nel centro del quadrato ne occupa metà della superficie. Sapendo che i quadrati sono equivalenti, determina il rapporto R/r.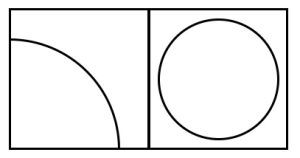
1. SOLUZIONE. L’area del quarto di cerchio a sinistra è πR2/4; mentre l’area del cerchio di destra è πr2. Definendo S l’area di ogni quadrato, avremo: πR2/4 = S/2 = πr2 [con R, r >0] che diviene R2/4 = r2. Infine R/r = 2.
2. Un’impresa industriale, con una capacità annua di 180.000 unità di prodotto alfa, sostiene costi fissi su base annua per l’importo complessivo di euro 230.000 e un costo variabile unitario di euro 7. Il prezzo unitario di vendita è di euro 13. Determinare:
2. SOLUZIONE. a) Il punto di equilibrio si calcola mettendo a rapporto i costi fissi con la differenza tra prezzo unitario e costo variabile unitario, nel nostro caso: 230.000 / (13 – 7) ≈ 38.333 (quantità di prodotti per l’equilibrio).
b) Il grado di sfruttamento degli impianti è (38.333 / 180.000)* 100 = 21,3%.
c) la quantità di produzione necessaria per un utile di euro 100.000 è (230.000 + 100.000) / (13 – 7) = 55.000 unità di prodotto alfa.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
6 risposte
Wonderful article! We will be linking to this particularly great
post on our website. Keep up the great writing.
I really like your blog.. very nice colors & theme. Did you make this website yourself or did you hire someone to do it for you?
Plz respond as I’m looking to construct my own blog and would
like to find out where u got this from. cheers
Ecco il disegno 🙂 (prima non avevo geogebra sottomano…)
Diciamo che il mio approccio alla matematicaè sempre stato lo sporcarsi le mani per vedere se c’è un esempio semplice da cui tirare fuori una soluzione globale. E come ogni buon matematico sono abbastanza pigro e quindi cerco di evitare di fare conti, se possibile!
Molto bello. Tks.
per il primo problema c’è un metodo forse più semplice. Costruiamo due quadrati 2×2: nel primo mettiamo quattro copie ruotate del quadrato di sinistra per ottenere un unico cerchio, nel secondo quattro copie del quadrato di destra. Il cerchio grande del primo quadrato ha la stessa area dei quattro cerchi piccoli del secondo quadrato, quindi il rapporto dei due raggi è √4 = 2.
Soluzione visionaria, ottima merita un disegno. Onorato di aver un suo commento, ammiro il suo approccio alla matematica, ai giochi logici e alla musica.