40. Soluzioni del 18 aprile 2022 – Cinque automobili alla rotatoria

Le soluzioni del 18 aprile 2022 a cura di Fabio Ciuffoli 

Nella prima mattinata di ieri abbiamo proposto un gioco logico deduttivo con cinque piloti. Ora pubblichiamo la soluzione e la dimostrazione. 

Cinque automobili alla rotatoria

Cinque automobili stanno girando intorno a una rotatoria a Londra. In sequenza i piloti sono: Alvin, Ben, Charles, David e Ernest. Le auto hanno targhe numerate 1, 2, 3, 4 e 5, ma non necessariamente in questo ordine. Ogni conducente può vedere la targa dell’auto che ha davanti e quella dietro, ma non dell’auto che sta guidando. Tutti i conducenti possono parlare e ascoltarsi tramite audiocuffie.

Una voce arriva alle loro cuffie e chiede: “La tua targa è un numero quadrato?” [un numero quadrato è un numero intero che è il quadrato di un altro numero intero, nel nostro caso i numeri sono: 1 e 4]

Tutti rispondono: “Non lo so”.

La voce ripete: “La tua targa è un numero quadrato?”

Rispondono: “Non lo so!” ad eccezione di Ernest che dice: “No.”

La voce chiede: “La tua targa è più grande del numero della targa dietro di te?”

David: “Non lo so!”

A questo punto Ben ed Ernest dicono: “No”. E Alvin e Charles dicono: “Sì”.

Con quale targa viaggia ciascun conducente?

[I piloti sono tutti ottimi logici. Attenzione, siamo a Londra e le rotonde si percorrono in senso orario.]

SOLUZIONE.

Passo 1. Le vetture sono disposte in cerchio e numerate da 1 a 5. Alla domanda se la loro targa sia un numero quadrato, ovvero 1 o 4, tutti i conducenti rispondono “Non lo so”. Per rispondere in questo modo, occorre che ciascun pilota non veda, davanti e dietro, la combinazione di numeri 1 e 4, altrimenti risponderebbe “No”, perciò si può escludere che ci sia un’auto tra la 1 e la 4, quindi la 1 e la 4 devono essere adiacenti.

Passo 2. La stessa domanda viene posta di nuovo, “la tua targa è un 1 o un 4” e Ernest dice di no. Dalle risposte alla prima domanda, si sa che la 1 e la 4 sono adiacenti e se Ernest risponde “no” significa che non vede né 1 né 4. Si può quindi dedurre che Ernest sia nella posizione opposta alla 1 e alla 4 e poiché è noto l’ordine dei piloti, la 1 e la 4 devono essere guidate da Ben e da Charles, mentre la 2, 3 e 5 da Alvin, David e Ernest, come illustrato in figura.

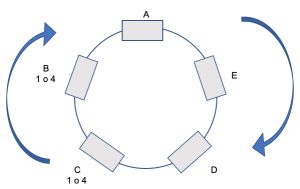
Passo 3. La voce chiede se la targa del conducente è più grande di quella dietro. David dice di non saperlo, ma sa dai passi 1 e 2 che la 1 è pilotata da Ben o Charles, quindi si può dedurre che non vede la 2 dietro di sé, perché se così fosse saprebbe che la sua è più grande e avrebbe risposto “sì”. Si può dedurre anche che non vede la 5, perché altrimenti avrebbe risposto “no”. Quindi David vede la targa 3 che è dell’auto pilotata da Ernest. Invitiamo il lettore a completare la figura inserendo, man mano, le informazioni.

Ben, che ha Charles dietro di sé, risponde che il suo numero non è più grande di quello di Charles, quindi vede la 4 di Charles e si può dedurre che Ben avrà la 1.

Charles, che sa di avere la 4 e vede la 1 davanti a sé, dice che il numero dietro di lui è inferiore a 4. Quindi David non ha la 5, così Alvin deve avere la 5 e infine David avrà la 2.

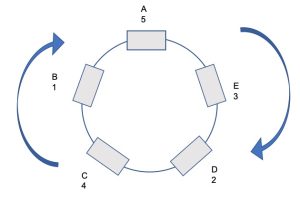
Il risultato finale: Alvin 5, Ben 1, Charles 4, David 2 ed Ernest 3.

A lunedì prossimo.