4. Soluzioni del 2 agosto 2021 – Probabilità e figlie di nome Wanda

Le soluzioni del 2 agosto 2021 a cura di Fabio Ciuffoli 

Probabilità e figlie di nome Wanda – soluzioni

(Assumiamo che le signore Albi, Bianchi, Carli, Dini e Ermeti siano scelte casualmente dalla popolazione di famiglie con due figli e che la probabilità di nascere maschio o femmina sia 50/50, di nascere in qualsiasi giorno della settimana sia 1 su 7 e in qualsiasi giorno dell’anno sia 1 su 365, escludiamo gli anni bisestili).

1. La signora Albi ha due figli, il più grande è una femmina. Qual è la probabilità che entrambi siano femmine?

1. SOLUZIONE. La probabilità che entrambe siano femmina è del 50%. Se il più grande è femmina, il più giovane può essere maschio o femmina, quindi lo spazio campionario è FF – FM con uguali probabilità di 1 su 2.

2. La signora Bianchi ha due figli e almeno uno è una femmina. Qual è la probabilità che entrambi siano femmine?

2. SOLUZIONE.  La probabilità che entrambe siano femmine è del 33%. Se almeno uno è femmina, cambia il contesto rispetto al problema precedente e lo spazio campionario diventa FF – MF – FM (va esclusa la combinazione MM) e tra queste tre combinazioni, una è quella richiesta, per cui 1 su 3.

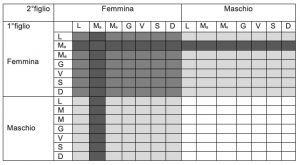
3. La signora Carli ha due figli e almeno uno è una femmina nata di martedì. Qual è la probabilità che entrambi siano femmine?

3. SOLUZIONE. La probabilità che entrambi i figli siano femmine è del 48%. Strano e controintuitivo!! Rispetto al problema precedente è stata aggiunta l’informazione, apparentemente irrilevante, “nata di martedì” e la probabilità è decisamente cambiata dal 33% al 48%. Infatti, come vedremo, le informazioni aggiuntivi cambiano le probabilità. Il diagramma mostra tutte le possibili combinazioni di sesso e giorno, sia per il primo che per il secondo figlio: è lo spazio campionario completo, nel quale ciascuna delle 196 caselle (14 x 14) è ugualmente probabile. Il quadrante in alto a sinistra, grigio medio a parte per alcune caselle più scure, contiene 49 quadrati e corrisponde all’evento “entrambi femmine” con probabilità 49/196 = ¼ come ci aspettavamo. L’informazione “almeno uno è femmina nata di martedì” riduce lo spazio campionario alle sole due strisce grigio scuro composta da 27 caselle, 14 orizzontali e 14 verticali meno 1 per la sovrapposizione, per non contare due volte lo steso evento. Contiamo ora quante caselle scure si trovano nella regione che ci interessa “femmina-femmina”: la risposta è 13 (7 + 7 – 1). Deduciamo quindi che la probabilità condizionata che la signora Carli abbia due femmine, posto che almeno un figlio è femmina nata di martedì, è 13/27, il 48,15%. Il giorno di nascita ha importanza!

La formula algebrica. Definiamo n il numero dei giorni della settimana in cui è nata la figlia, ad esempio nel nostro caso “nata di lunedì” quindi n = 1, se fosse “nata di lunedì o martedì” sarebbe n = 2 e via di seguito fino a “non nata di lunedì” con n = 6 e infine, “nata in qualsiasi giorno della settimana” con n = 7, quindi simile al problema 2, avremo:

[2*7*n – (n^2)] / [2*7*n – (n^2) + 2*7*n]

con n = 1 avremo (14 – 1) / (13 + 14) = 13/27 = 48,15%

con n = 2 avremo 24/52 = 46,15%

… …. …

con n = 6 avremo 48 /132 = 36,36%

infine con n = 7 avremo  49 / 147 = 33,33% esattamente come nel problema 2.

4. La signora Dini ha due figli, almeno uno è femmina nata il primo aprile. Qual è la probabilità che entrambi siano femmine?

4. SOLUZIONE. La probabilità che entrambi siano femmine è 729/1459 o circa il 50%. I calcoli sono simili a quelli precedenti. Nel diagramma ogni quadrante è 365 x 365. Le strisce scure, in ogni quadrante, contengono 365 quadrati ciascuna, ma si sovrappongono in una casella. All’interno della regione bersaglio “femmina-femmina” avremo 365 + 365 – 1 = 729 quadrati scuri. Ci sono 365 + 365 = 730 quadrati scuri all’esterno del bersaglio e quindi il totale dei quadrati scuri è 729 + 730 = 1.459. La probabilità condizionata che signora Ermini abbia due femmine, posto che almeno un figlio è femmina nata il primo aprile, è 729/1.459, cioè circa 49,97%. Nella formula algebrica, vista sopra, sostituiremo il 7 con 365.

5. La signora Ermeti ha due figli, almeno uno è una femmina di nome Wanda. Qual è la probabilità che entrambi siano femmine?

5. SOLUZIONE. La probabilità che entrambi siano femmine è precisamente del 50%. La legge italiana vieta di chiamare due sorelle viventi con lo stesso nome, per cui non avremo le sovrapposizioni nel quadrante F-F. Nella formula algebrica scompare n^2. Il risultato è sempre 50% qualsiasi nome venga scelto.

Per riassumere: quando non viene specificato l’ordine di nascita (caso 2) la probabilità che entrambi siano femmine è del 33%; più informazioni vengono fornite – come il giorno di nascita (caso 3) la data di nascita (caso 4) il nome abbastanza raro (caso 5) – più aumentano le probabilità, fino a avvicinarsi al 50%. Quando viene specificato l’ordine di nascita (caso 1) le probabilità sono esattamente del 50%.

A lunedì prossimo.