
I giochi del lunedì di Prisma del 4 aprile 2022 – a cura di Fabio Ciuffoli
Oggi presentiamo sei problemi di geometria, a difficoltà crescente, tratti da Maths, Reasoning, Knowledge, un ottimo gruppo di divulgazione matematica con più di 60.000 iscritti e una trentina di amministratori. Invitiamo i lettori a presentarci osservazioni e proposte di soluzione nello spazio riservato ai commenti. Domani pomeriggio alle 17.00 pubblicheremo le soluzioni con le dimostrazioni.
Geometria da Maths, Reasoning, Knowledge
1. Determinare l’area colorata in blu, sapendo che AB unisce i punti medi dei due lati del rettangolo.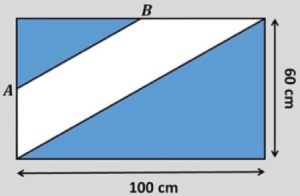
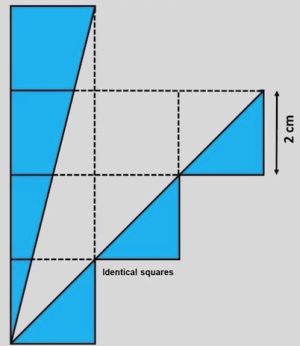
2. Determinare l’area colorata in blu.
3. Nella figura sono disegnati quattro cerchi con raggio rispettivamente di 6 cm, 4 cm, 3 cm e 2 cm. Determinare l’area colorata in blu.
4. Determinare l’area ombreggiata in blu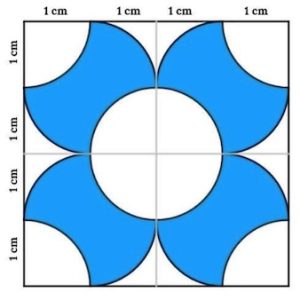
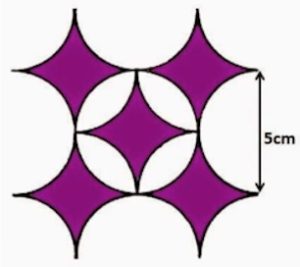
5. Determinare l’area ombreggiata in viola.
6. Dal cubo con spigoli di 10 cm è stato tagliato il pezzo blu. Calcolare il volume della parte rimossa, sapendo che il taglio passa per i punti medi dei tre spigoli adiacenti.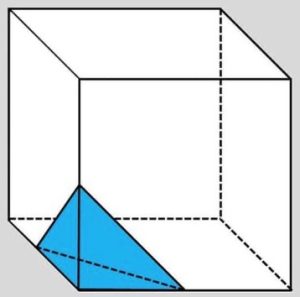
Aggiornamento per le soluzioni click qui
I problemi sono stati proposti da Dwi Kristina della Airlangga University di Surabaya in Giava Orientale, che ringraziamo per la collaborazione e ci ricorda che le immagine originali sono tratte da Pibyme Official.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
15 risposte
Vedi allegati:
1)
2)
3)
4)
5)
6)
Perfetto. Oggi pomeriggio le soluzioni con un paio di dimostrazioni di tipo “analogico”.
1) dividendo il rettangolo unendo i punti medi dei lati, ottengo 4 rettangoli più piccoli, di cui uno tutto colorato e gli altri 3 colorati per metà:
– (50×30) x1 + ((50X30)/2) * 3 = 1500 + 2250 = 3750 cm2
2) un’area è la metà di un rettangolo di area 2×8, le altre sono metà di quadrati 2×2, quindi:
– (8×2)/2 + ((2×2)/2) * 3 = 8 + 6 = 14 cm2
3) l’area colorata maggiore è (6x6xpi)-(4x4xpi); quella minore è (3x3xpi)-(2x2xpi), quindi sommando:
– (36pi-16pi) + (9pi-4pi) = 20pi+5pi = 25 pi cm2
4) divido la figura unendo i punti medi dei suoi lati, ottengo 4 quadrati, e faccio la stessa operazione, ottenendone 16 quadrati. Considero uno dei quattro, e noto che le figure blu, sommate due a due, danno due quadrati di lato (1×1) cm2, quindi:
– per quattro quadrati, ho 2 x 4 = 8 cm2
5) ogni area viola è la differenza tra l’area di un quadrato di lato 5 cm e un cerchio di raggio 2,5 cm, quindi:
– 25-(25/4)pi cm2 per ogni area; per cinque aree, (25-(25/4)pi) * 5 cm2 = (125-(125pi/4)) cm2
6) l’area di base della piramide così delimitata è (5×5)/2 = 12,5 cm2, il volume è base per altezza, quindi:
– 12,5 * 5 = 62,5cm3; ma per una piramide devo dividere per 3, quindi 62,5/3 = 20,83 cm3
Perfetto. Oggi pomeriggio le soluzioni.
1. Molto semplicemente, notando (vedi disegno allegato) che dividendo il rettangolo in 8 triangoli uguali l’area blu corrisponde a 5 di questi triangoli, l’area cercata è uguale a 5/8 dell’area del rettangolo, ovvero 60 * 100 * 5/8 = 3750.
2. Nello stesso modo notiamo che l’area blu è composta di triangoli che sono ricavati dividendo in due rettangoli che sono modulari del quadrato base. Quindi contiamo i quadrati interessati, e calcoliamo l’area cercata divideno per due l’area dei quadrati. 4 quadrati formano il rettangolo grande, più 3 quadrati “singoli” = 7 quadrati. L’area dei quadrati è 7 * 4 = 28. 28 / 2 = 14 che è l’area cercata.
6. Innanzitutto dividiamo il cubo grande in 8 cubi tagliandolo a metà in tutti i lati. La piramide di cui vogliamo trovare il volume si trova in uno di questi cubi più piccoli ed i vertici della piramide coincidono con altrettanti vertici del cubo. Il volume del cubo piccolo è uguale a 1/8 del volume del cubo grande. Ora seghiamo il cubo piccolo a metà tagliandolo sulla diagonale di una faccia ed otteniamo un prisma triangolare regolare la cui base coincide con quella della piramide. Il volume del prisma è uguale ad 1/2 del volume del cubo piccolo, ovvero 1/8 * 1/2 = 1/16 del volume del cubo grande. Il volume della piramide che stiamo cercando deve essere uguale a 1/3 del volume del prisma, per cui 1/16 * 1/3 = 1/48 del volume del cubo grande. 10 * 10 * 10 / 48 = 20,8333…
(Ovviamente bastava calcolare il volume della piramide direttamente con le misure note…)
Perfetto a domani per tutte le soluzioni con le dimostrazioni, a volte anche originali almeno spero.
Quesito 5: i bordi curvi, sommati, hanno area uguale a quella di una una “stella”; l’area totale vale 5 stelle cioè 5(Q-C), con Q quadrato di lato 5 cm e C cerchio di raggio 5/2 cm. L’area vale dunque 5(25 – 25/4 π) cm² cioè (125 – 125/4 π) cm².
Ottimo, a domani per tutte le soluzioni.
Problema 1: si tratta di sommare l’area di due triangoli rettangoli. Uno (T1) è la metà del rettangolo, l’altro (T2) ha i due cateti pari a 50 e 30 cm. Pertanto T1=3000 cm^2, T2= 750 cm^2 e l’area blu vale 3750 cm^2.
Problema 2: L’area blu è pari a un triangolo avente area metà del rettangolo 4×1 posto verticalmente, più 3*1/2 dell’area di un quadrato. Quindi l’area blu vale 8 cm^2 + 3/2 * 4 cm^2 = 14 cm^2.
Problema 3: Indicando con A1, A2, A3, A4 le aree dei 4 cerchi in ordine decrescente di dimensione, si trova che l’area in blu è pari a: A1-(A2-A3)-A4 = pi*(36-(16-9)-4)=25*pi cm^2.
Problema 4: Per simmetria ci concentriamo su uno dei 4 quadranti. L’area del quadrato è 4 cm^2 a cui vanno sottratte le 4 aree non colorate. Queste quattro aree sono divise in due gruppi da due, A1 e A2. A1 vale un quarto dell’area del cerchio di raggio 1, ovvero A1= pi/4. A2 vale 1/4 della differenza tra l’area del quadrato e l’area del cerchio di raggio 1, ovvero A2 = 1-pi/4. Pertanto, il singolo quadrante avrà un’area blue B1= 4 – 2*(pi/4+1-pi/4) = 4-2 = 2 cm^2. Dato che i quadranti sono 4, questo numero va moltiplicato per 4. L’area blu totale vale 8 cm^2.
Perfetto