35. Soluzioni del 14 marzo 2022 – La Scuola di Leopoli

Le soluzioni del 14 marzo 2022 a cura di Fabio Ciuffoli

Ieri mattina abbiamo proposto due problemi in omaggio alla Scuola Logica di Leopoli e di seguito presentiamo le soluzioni con e le dimostrazioni.

La Scuola di Leopoli – soluzioni 

1. Tre amici contribuiscono ciascuno con 40 euro per comprare un formaggio da 120 euro. Il primo amico lo divide in tre parti, affermando che i pesi sono uguali. Il secondo amico, che non si fida del primo, pesa di nuovo i pezzi e li giudica del valore di € 30, € 40 e € 50. Il terzo, diffidente nei confronti di entrambi, pesa il formaggio sulla propria bilancia, ottenendo un diverso risultato. Ogni amico sostiene che la sua pesata è corretta, come possono dividere i pezzi, senza tagliarli di nuovo, in modo tale che ciascuno possa ammettere di aver ricevuto almeno € 40 di formaggio?

1. SOLUZIONE. Il terzo amico deve credere che uno dei pezzi valga almeno la media, ossia € 40, perché se non lo facesse, il totale di tutti i pezzi non ammonterebbe a € 120 e perciò prenderà quel pezzo. Ora sono rimasti due pezzi e il secondo amico può scegliere uno di questi al quale deve aver attribuito il valore di almeno € 40. Ad esempio, se il secondo amico avesse attribuito i valori di 35, 45 e 50 potrà scegliere tra due valori, di cui uno sarà sempre uguale o superiore a € 40. Infine il primo amico prende il pezzo rimanente, che secondo lui vale € 40.

2. Dieci rubini e quattordici diamanti sono incastonati, in ordine casuale, su una collana. Dimostrare che è possibile tagliare la collana in due punti, in modo che ognuno dei due pezzi abbia metà dei rubini e metà dei diamanti.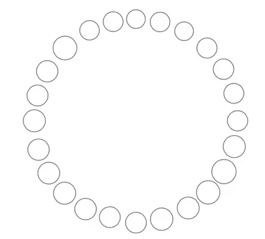

2. SOLUZIONE. Esistono più di 40.000 combinazioni di collane in grado di soddisfare le condizioni poste dal testo, tuttavia, in base al teorema del valore intermedio, il problema ha sempre una soluzione per qualsiasi numero pari di rubini e di diamanti. Immaginiamo la collana disposta su una circonferenza, con le 24 pietre equidistanti, colorate di rosso e di rosa.

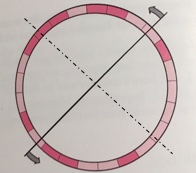
Tracciamo una linea attraverso il centro della circonferenza, in modo da individuare due semicirconferenze con 12 pietre ciascuna. Ovviamente potrebbero esserci più rubini su un lato che sull’altro. Ipotizziamo, come in figura, che ci siano più rubini alla sinistra della linea, quindi ruotiamo gradualmente la linea in senso antiorario fino a ottenere due semicirconferenze con lo stesso numero di rubini, nel nostro caso 5 da una parte e 5 dall’altra, vedi linea tratteggiata. A questo punto se ci sono 5 rubini in una semicirconferenza, significa che su quella semicirconferenza, ci saranno anche 7 diamanti. Contemporaneamente avremo 5 rubini e 7 diamanti sull’altra circonferenza e così abbiamo risolto il problema.