
Le soluzioni del 31 gennaio 2022 a cura di Fabio Ciuffoli
Ieri abbiamo proposto cinque problemi che prevedono diversi metodi per la soluzione e di seguito presentiamo i relativi procedimenti.
Affidarsi agli occhi e affidarsi ai conti – soluzioni
1. ABC è un triangolo rettangolo dove l’ipotenusa AC è il diametro della circonferenza più grande. I cateti misurano 8 cm e 15 cm. Quanto vale la somma dei diametri delle due circonferenze?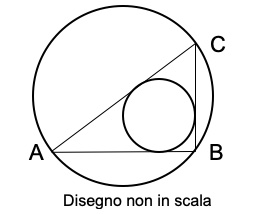
1. SOLUZIONE. Presentiamo due metodi: il primo si basa sull’intuizione e la percezione visiva, mentre il secondo si affida alla riflessione e ai calcoli.
Primo metodo. Con il teorema di Pitagora si calcola l’ipotenusa di 17 cm. Osserviamo che i segmenti di tangenza dal punto A alla circonferenza piccola sono uguali e lo stesso accade per i segmenti dal punto B e C.
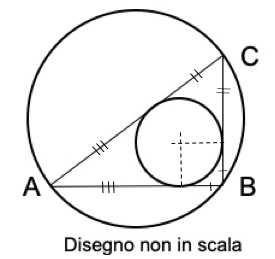 Sottraendo quindi dalla somma dei due cateti la lunghezza dell’ipotenusa, restano i due segmenti di tangente uscenti dal vertice B dell’angolo retto, che sono uguali al raggio della circonferenza piccola.Si può determinare, senza altri calcoli, che il diametro della circonferenza più piccola è 8 + 15 – 17 = 6 cm.
Sottraendo quindi dalla somma dei due cateti la lunghezza dell’ipotenusa, restano i due segmenti di tangente uscenti dal vertice B dell’angolo retto, che sono uguali al raggio della circonferenza piccola.Si può determinare, senza altri calcoli, che il diametro della circonferenza più piccola è 8 + 15 – 17 = 6 cm.
Secondo metodo: Dopo aver calcolato l’ipotenusa di 17 cm ragioniamo sul triangolo ABC che è circoscritto alla circonferenza più piccola e, come in tutti i poligoni circoscritti, l’area del poligono si può calcolare con la nota formula “Area = perimetro per apotema diviso 2”. In questo caso l’apotema è il raggio della circonferenza inscritta, il perimetro è 8 + 15 + 17 = 40 cm e quindi l’area del triangolo è (8 * 15) /2 = 60 cm2. Ora applicando la formula inversa con incognita l’apotema, “Apotema = (Area * 2 ) / perimetro”, avremo: (2 * 60) / 40 = 3 cm che è il raggio e quindi il diametro è 6 cm.
Infine la somma dei diametri delle due circonferenze è 17 + 6 = 23 cm.
2. L’area del quadrato è 225 cm2 divisa in nove quadratini uguali tra loro. La stella è stata costruita congiungendo i vertici del quadrato con i punti medi dei lati del quadratino centrale. Quanto vale l’area della stella?

2. SOLUZIONE. L’area della stella è data dalla differenza tra l’area dell’intero quadrato e l’area dei quattro triangoli azzurri uguali tra loro. In ogni triangolo azzurro, la misura della base è quella del lato del quadrato (15 cm) e la misura dell’altezza è 1/3 di quella del lato del quadrato (5 cm). Quindi l’area della stella è 225 – (4 * 15 * 5) / 2 = 75 cm2.
Una soluzione che si “affida più agli occhi che ai conti” si basa sull’osservazione dell’area di ciascuno dei triangoli azzurri che è 1/6 dell’area del quadrato. L’area dei quattro triangoli azzurri è 4/6 quindi 2/3 dell’area del quadrato, perciò l’area della stella è 1/3 dell’area del quadrato quindi 225/3 = 75 cm2.
3. Quanto vale l’area del quadrato grigio, sapendo che l’area del quadrato a puntini è un quarto dell’area del quadrato grande?
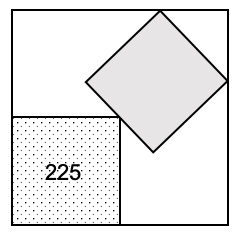
3. SOLUZIONE. Nel disegno mostriamo che il quadrato grigio è composto da quattro piccoli triangoli, inoltre nove di loro costituiscono una metà del quadrato grande. L’area del quadrato grigio è quindi: [(225/2) * 4 / 9] * 4 = 200 cm2. Più in generale, il rapporto tra area grigia e area puntinata è 8/9.
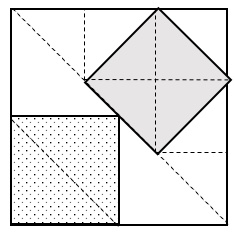
4. All’interno del quadrato in figura è stato disegnato un triangolo. Qual è il rapporto tra l’area del triangolo e l’area del quadrato?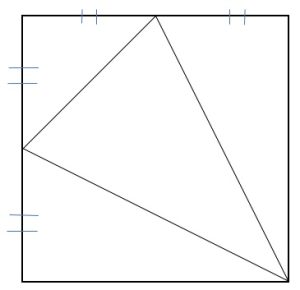
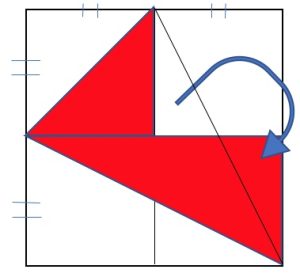
4. SOLUZIONE. Osservando la figura si può vedere che il triangolo rosso, appositamente scomposto, occupa 1/8 + ¼ = 3/8 del rettangolo. Lasciamo al lettore individuare altri metodi basati sul calcolo di aree dei triangoli e dei quadrati.
5. Il puzzle, in figura a sinistra di chi legge, è stato costruito dividendo un quadrato di lato 24 cm con due segmenti perpendicolari tra loro e passanti per il centro del quadrato. I quattro pezzi del quadrato così ottenuti possono essere assemblati di nuovo per formare l’altro quadrato, con un buco nella regione centrale, a destra in figura. Quanto misura in cm il lato del nuovo quadrato?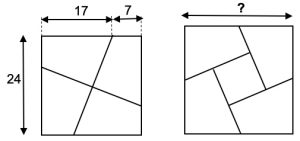
5. SOLUZIONE. Il primo quadrato presenta un’evidente simmetria rispetto al suo centro e si vede che è diviso in quattro quadrilateri uguali, ciascuno dei quali ha due lati che misurano 7 e 17 cm. Ciascun semitaglio si può calcolare con il teorema di Pitagora. Il semitaglio è l’ipotenusa di un triangolo rettangolo di cateti 12 e 5 cm e misura 13 cm, come mostrato in figura.
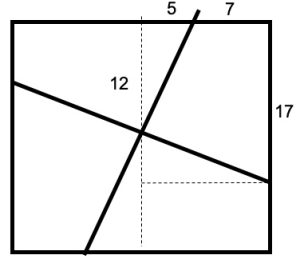
Ciascuno dei quattro quadrilateri ha due angoli retti nei quali confluiscono: i due lati 7 e 17 cm e due semitagli lunghi ciascuno 13 cm. Il quadrato di destra è più grande perché ai quattro pezzi del puzzle si è aggiunto un nuovo quadrato. Nei vertici del quadrato di destra non possono allora confluire i lati di 7 e 17 cm, perché altrimenti il quadrato di destra avrebbe le stesse dimensioni di quello precedente. Vi confluiscono dunque i due semitagli da 13 cm, perciò il lato del nuovo quadrato è 26 cm. Ovviamente l’area del quadrato interno è 100 cm2 e il suo lato 10 cm.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
2 risposte
Per il problema 5, Thomas Paoloni: “Si vede subito anche ad occhio, dal modo in cui sono appoggiate le figure tra loro che il quadrato all’interno ha il lato dato dato da 17 – 7 = 10
L’area del nuovo quadrato sarà quindi data dall’area del vecchio più questo quadratino (noto) ricavato all’interno, il lato del nuovo quadrato è facilmente calcolabile eseguendo la radice quadrata della nuova area. L’area totale sarà 24*24 + 10*10 = 576+100 = 676
Il lato invece radice di 676 = 26”. Allego disegno
Ringrazio tutti i partecipanti per i commenti inviati, in particolare quelli che hanno scritto sul blog. Desidero in ogni caso segnalare alcuni interessanti interventi, tra questi:
per il problema 1, Michele Rossi: “Naturalmente 23 cm, ovvero la somma dei due cateti.
Ma si può generalizzare dicendo che, per qualsiasi triangolo rettangolo, la somma dei diametri relativi rispettivamente alla circonferenza inscritta e alla circonferenza nella quale può essere inscritto il triangolo stesso, è sempre uguale alla somma dei cateti.”
Per il problema 2, Massimo Molinelli di cui allego l’ottimo disegno.