
Le soluzioni del 10 gennaio 2022 a cura di Fabio Ciuffoli
Ieri mattina abbiamo presentato quattro problemi e ora pubblichiamo le soluzioni con le relative dimostrazioni algebriche e grafiche.
Due tavoli, un quadrato e due cerchi – soluzioni

SOLUZIONE. Presentiamo due soluzioni, una algebrica e l’altra grafica. Algebrica: indichiamo con T l’altezza del tavolo, con G l’altezza del gatto e con t l’altezza della tartaruga e avremo il seguente sistema:
Sommando membro a membro otteniamo 2 T = 60 e infine T = 30 cm. L’altezza della tartaruga e del gatto sono indeterminate: l’altezza del gatto è maggiore di 4 cm dell’altezza della tartaruga e minore dell’altezza del tavolo (30 cm meno lo spessore del piano del tavolo); la tartaruga è maggiore di zero e minore (dell’altezza del tavolo meno lo spessore del piano del tavolo, meno 4 cm, meno l’altezza del gatto).
Per la soluzione grafica visiva, tagliamo in verticale a metà il tavolo e poniamo la parte alla nostra sinistra in alto sulla parte alla nostra destra in modo da far coincidere le due tartarughe. Vedremo così l’altezza dei due tavoli, data dalla somma 26 + 34 = 60, quindi un tavolo è alto 30 cm.
Segnaliamo inoltre che l’altezza del tavolo e degli animali è inverosimilmente piccola, ciononostante la doppia procedura di soluzione mostra un suo fascino.
2. Calcolare l’altezza del tavolo

2. SOLUZIONE. Indichiamo con T l’altezza del tavolo, con G l’altezza della gallina e con P l’altezza del pulcino e avremo il seguente sistema:
Risolvendo avremo: 3T = 60 + 60 + 45 e infine T = 165/3 = 55 cm.
3. Calcolare l’area rossa.

3. SOLUZIONE. Anche per questo problema proponiamo una soluzione grafica e una algebrica. Grafica visiva: spostando i due semicerchi rossi dalla parte superiore a quella inferiore, come mostrato in figura ci si accorge che l’area rossa è metà dell’area del quadrato. L’area rossa è quindi 8 * 4 = 32 cm2.
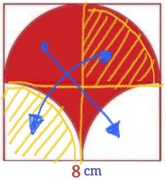
Algebrica: (l’area del semicerchio rosso) + (la metà dell’area del quadrato meno i due quarti del cerchio bianchi). In cifre (½ * 42 * π) + (½ * 82 – ½ * 42 * π) = 8π + 32 – 8π = 32 cm2.
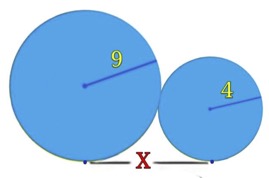
4. Calcolare la lunghezza del segmento x.
4. SOLUZIONE. Il segmento che congiunge i due centri delle circonferenze misura 13 ed è l’ipotenusa di un triangolo rettangolo con un cateto che misura 5 e l’altro cateto che misura x. Con il teorema di Pitagora avremo x2 = 132 – 52 quindi x = √ 144 = 12.
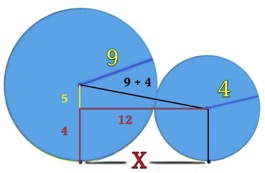
Il disegno non è in scala.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Ho ricevuto numerosi commenti, prevalentemente sui problemi 1 e 2, da parte di diversi lettori che ringrazio per la partecipazione. Di seguito ne riporto alcuni.
Sul problema 1 con Tavolo, Gatto e Tartaruga
Raffaele Luperto: Credo che la soluzione sia da fornire come parametrica (vedi Rouchè-Capelli).
Se chiamiamo t l’altezza della tartaruga, g quella del gatto e H l’altezza del tavolo abbiamo:
g + H – t = 34
t + H – g = 26
che ci forniscono H = 30, da cui:
g = t + 4
Quindi:
(t, g, H) = (t, t + 4, 30) con t, g < 30
Andrea Ruggiu: Indicando per brevità l'altezza dell'animale/oggetto con il nome dell'animale/oggetto stesso, otteniamo
Gatto + Tavolo – Tartaruga = 34cm
Tartaruga + Tavolo – Gatto = 26cm
Da cui, sommando e sottraendo le due equazioni si ottiene
2*Tavolo = 60cm
2*(Gatto – Tartaruga) = 8cm
Ovvero Tavolo = 30cm, Gatto = Tartaruga + 4cm. E del resto con due equazioni in tre incognite potevamo aspettarci poco altro, a meno di casi degeneri…
Nota: per verificare che non ci stiamo perdendo una condizione aggiuntiva, possiamo considerare due casi palesemente assurdi. Se la tartaruga fosse "infinitesima", ovvero se avesse altezza nulla (schiacciata con forza come una michetta bidimensionale – non fatelo davvero, però), ci ritroveremmo con un gatto alto 4 cm e l'iconografica sarebbe comunque giusta. Se invece, sempre considerando una situazione "patologica", la tartaruga fosse alta quanto il tavolo (30cm), ci ritroveremmo lo stesso con entrambe le condizioni del disegno soddisfatte.
Carlo Tieri: T + g – t = 34; T + t – g = 26. Quindi g – t = 34 – T; g – t = T – 26 Quindi 2(g- t) = 8; g – t = 4. Quindi T= 30. Ma g e t qualsiasi (OK, maggiori di zero e minori di T) come intuibile dalla figura mettendo gatto e tartaruga più alti o più bassi della stessa quantità. Tre incognite, due equazioni.
Antonio Tognon: Si può dire con certezza che il tavolo è alto 30 cm e che il gatto è alto 4 cm più della tartaruga, ma non si può stabilire con esattezza né l'altezza del gatto, né quella della tartaruga. Teoricamente, esistono infinite soluzioni possibili per gatto e tartaruga.
Davide Morgante: Tre incognite, due variabili. Usando Rouche-Capelli si mostra che il sistema ha 1-infinito soluzioni (lo spazio vettoriale generato dalle soluzioni ha dimensione 1), per cui possiamo determinare con certezza una sola variabile, le altre due dipenderanno l'una dall'altra.
Sul problema 2 con Tavolo, Gallina, Pulcino e Uovo
Antonio Misericordia: Sono 3 equazioni e 2 disequazioni in 4 incognite:
T + U = 60
T + G – P = 60
T + P – G – U = 45
da cui T = 55, U = 5
Per il resto sappiamo solo che il Pulcino è alto 5 centimetri meno della Gallina e che la Gallina è alta meno di 50 centimetri. Si può anche dedurre che il pulcino è alto meno della metà del tavolo e che (uovo+gallina) sono alti più della metà del tavolo, ma nulla più.
Grazie per la collaborazione.