Menu
Le soluzioni del 29 novembre 2021 a cura di Fabio Ciuffoli
Ieri mattina abbiamo proposto due giochi logici, con un livello di difficoltà crescente e ora presentiamo le soluzioni con dimostrazione.
L’equipaggio e gli appuntamenti serali – soluzioni
1. L’equipaggio. Alberto, Bruno e Carlo compongono un equipaggio di volo svolgendo le funzioni di pilota, copilota ed ingegnere, non necessariamente in tale ordine. Il copilota, che è figlio unico, guadagna meno di tutti. Carlo, che ha sposato la sorella di Bruno, guadagna più del pilota.
Qual è la posizione di ciascuno?
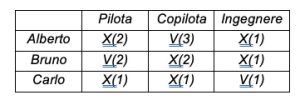
1. SOLUZIONE. Per risolvere questo problema utilizziamo una griglia 2D di misura 3×3, con in riga i nomi delle persone e in colonna le funzioni svolte, dove V indica una condizione di verità, mentre X indica una condizione di falsità. Tra parentesi sono riportati i numeri in sequenza delle considerazioni che presentiamo di seguito: (1) Carlo guadagna più del pilota e quindi, oltre a non essere il pilota, non è neppure il copilota perché quest’ultimo guadagna il meno di tutti, perciò Carlo è l’ingegnere e né Bruno né Alberto sono ingegneri; (2) A questo punto Bruno, che ha una sorella quindi non è figlio unico e perciò non può essere il copilota, deve essere il pilota; (3) Ora per eliminazione Alberto deve essere il copilota. In sintesi: Alberto è il copilota, Bruno il pilota e Carlo l’ingegnere.
2. Appuntamenti serali. Andrea, Berto, Cristiano e Daniele, ciascuno di loro ha un appuntamento serale con un’amica tra Emilia, Franca, Gina e Ilaria. Si sa che:
Chi uscirà con chi e che cosa faranno?
2. SOLUZIONE. Utilizziamo una griglia 3D di misura 4x4x4, come se guardassimo il cubo da un angolo vedendo tre facce e poniamo le quattro alternative sui tre spigoli. E’ questo l’omaggio indiretto al cubo di Rubik.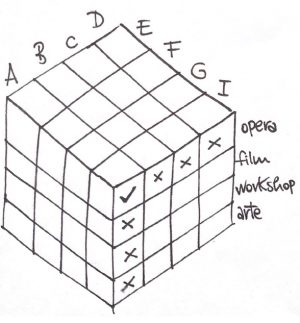 
Ora inseriamo le informazioni. L’affermazione 1 dice che Andrea va all’Opera, perciò mettiamo una spunta su Andrea/Opera che appare sulla faccia a destra. A questo punto escludiamo, mettendo una X, Andrea/film, Andrea/workshop e Andrea/arte. Escludiamo anche che Berto, Cristiano e Daniele non andranno all’opera, quindi mettiamo una X nelle celle corrispondenti. L’affermazione 2 dice che Berto va con Emilia, quindi nella faccia superiore spunteremo la cella Berto/Emila. Continuando in questo modo, riempiremo la griglia e ogni faccia avrà quattro spunte. Invitiamo il lettore a procedere autonomamente, infine avremo: Andrea e Ilaria vanno all’Opera, Berto e Emila visitano la mostra d’arte, Cristiano e Franca guardano un film, mentre Daniele e Gina partecipano al workshop.
A lunedì prossimo.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).
Una risposta
Segnalo un paio di interessanti proposte di soluzione con il relativo metodo.
Una inviata da Fabio Felici
a) Emilia, uscendo con Berto:
per 1. non andrà all’opera
per 4. non vedrà un film
per 5. non parteciperà a un workshop.
quindi, per esclusione, andrà ad una mostra d’arte e ci va con Berto.
b) Ilaria:
per 4. non vedrà un film
per 5. non parteciperà a un workshop
per a) non andrà alla mostra
quindi, per esclusione, va all’opera con Andrea.
c) Gina:
per 2. non esce con Cristiano
quindi per esclusione andrà al workshop con Daniele.
d) Franca:
per esclusione si vedrà un film con Cristiano.
Una seconda soluzione di Lucia Fogliato con grafico che allego
Grazie a Fabio Felici e Lucia Fogliata per aver partecipato.