121. Soluzioni del 22 aprile 2024 – Cerchi e triangoli sangaku

Le soluzioni del 22 aprile 2024 a cura di Fabio Ciuffoli

Ieri abbiamo presentato tre problemi di geometria sangaku e di seguito pubblichiamo le nostre soluzioni commentate. 

Cerchi e triangoli sangaku- soluzioni 

1. Ala e lente. Un quarto di cerchio contiene due semicerchi più piccoli come disegnato in figura. Dimostrare che la sagoma ad ala A ha la stessa area della sagoma a lente B.

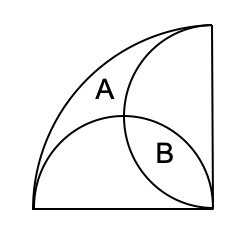
L’area del cerchio grande è πr². Il raggio dei cerchi più piccoli è metà del raggio di quello grande, per cui l’area di ciascun cerchio piccolo è π(r/2)² = πr²/4. I cerchi piccoli hanno ciascuno esattamente un quarto dell’area di quello grande e quindi la somma delle aree di quattro cerchi piccoli è uguale all’area del cerchio grande. I  cerchi piccoli, però, si sovrappongono in quattro spazi (area della lente B) e lasciano scoperto quattro spazi dell’area del cerchio grande (area dell’ala A). Per questa ragione le aree sovrapposte e le aree scoperte sono uguali e visto che sono quattro ali uguali e quattro lenti uguali, l’area di una singola ala è uguale all’area di una singola lente.   

2. Diciotto cerchi. L’immagine mostra cerchi di cinque dimensioni. Ci sono sei cerchi bianchi, sette grigio scuro, tre grigio chiaro, uno tratteggiato inscritto nel triangolo e uno più grande descritto da una linea continua. Qual è il rapporto tra il raggio del cerchio tratteggiato e il raggio di un cerchio bianco?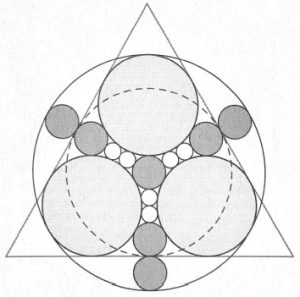

2. SOLUZIONE. Chiamiamo i cerchi dal più piccolo al più grande: A, B, C, D, E con i rispettivi raggi a, b, c, d, e. Nell’immagine a sinistra evidenziamo tre segmenti in nero: quello verticale è il raggio d, del cerchio tratteggiato, che corrisponde a quattro raggi a sommati con i tre raggi b, perciò (1) d = 4a + 3b. Allo stesso modo, gli altri due segmenti in nero sono entrambi raggi e, che si possono descrivere in termini di altri raggi, perciò (2) e = 4a + 5b infine (3) e = b + 2c. 

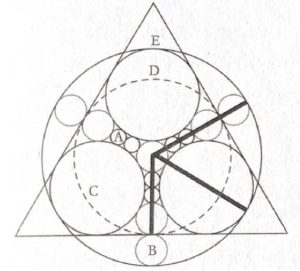
E ora l’intuizione! Disegniamo due triangoli equilateri con un lato in comune, evidenziati nella figura a destra. Gli angoli al centro di E sono di 60 gradi, i due lati opposti sono uguali e un lato è comune, quindi anche il terzo lato deve essere uguale. Il triangolo ha un vertice al centro di C perché lì si incontrano i due segmenti che partono dal centro dei cerchi B. Perciò (4) 4a + 2b = b + c.

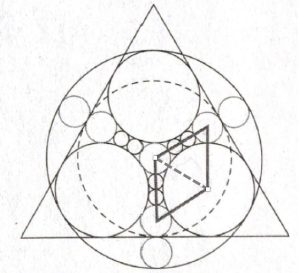
A questo punto uguagliamo la (2) e la (3)

4a + 5b = b + 2c   che diviene 4a + 4b = 2c   semplificando 2a + 2b = c

Inserendo nella (4) avremo: 4a + 2b = b + 2a + 2b   che diviene 2a = b.

Infine, sostituendo nella (1) avremo d = 4a + 6a = 10a   quindi il raggio d del cerchio tratteggiato è 10 volte il raggio del cerchio bianco.

3. Sei cerchi in un triangolo. Nella figura compaiono cerchi di tre diverse dimensioni: due neri, tre bianchi e uno grigio. Due cerchi neri e due bianchi sono inscritti in un quadrato. Il quadrato, insieme ad altri due cerchi, è collocato in un triangolo rettangolo. Dimostrare che il raggio del cerchio grigio è il doppio del raggio del cerchio nero.

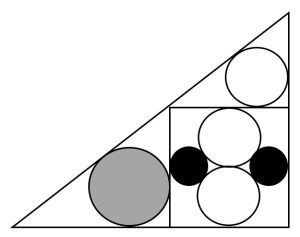3. SOLUZIONE. Indichiamo con A, B e C i cerchi in ordine crescente di dimensioni, con a, b, c i rispettivi raggi e calcoliamo dapprima b in termini di a, poi c in termini di b e infine mostriamo che c = 2a.

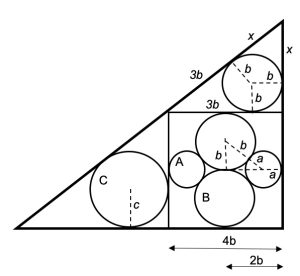
Il triangolo rettangolo, tratteggiato in figura, ha ipotenusa a + b mentre le lunghezze dei cateti sono b e (2b – a). La lunghezza (2b – a) si deduce rendendosi conto che la base del triangolo è lunga metà del lato del quadrato, ossia 4b/2, meno il raggio di A. Con il teorema di Pitagora avremo (a + b)² = b² + (2b – a)² diventa a² + 2ab + b² = b² + 4b² + a² – 4ab.

Raccogliendo e semplificando otteniamo 6ab = 4b² ora dividendo entrambi i membri per 2b avremo 3a = 2b e infine b = 3a/2 così abbiamo espresso b in termini di a.

Ora osserviamo il triangolo più in alto. Abbiamo tracciato tre raggi dal centro del cerchio verso ciascuno dei lati tangenti, quindi il triangolo è diviso in un quadrato b x b più due figure ad aquilone. Il lato lungo dell’aquilone a sinistra misura 3b, poiché è pari al lato del quadrato grande meno il raggio di B. Se chiamiamo x il lato lungo dell’aquilone in alto, con il teorema di Pitagora avremo:

(3b + x)² = (b + x)² + (4b)²  svolgendo  9b²  + x² + 6bx  = b² + x² + 2bx + 16b²

4bx = 8b² infine x = 2b.

Il lato verticale del triangolo superiore ha lunghezza x + b = 2b + b = 3b. Il lato verticale del triangolo sulla sinistra è 4b. Poiché i due triangoli sono simili, il rapporto tra i lati 3b/4b = ¾ sarà lo stesso del rapporto tra i raggi dei cerchi inscritti nei triangoli. Se ¾ = b/c allora c = (4/3)b. A questo punto abbiamo c in termini di b, inoltre abbiamo già espresso b in termini di a, quindi c in termini di a sarà: c = (4/3)b = (4/3) • (3a/2) = 12a/6 = 2a. Abbiamo così dimostrato che il raggio del cerchio grigio c è il doppio del raggio del cerchio nero a.  

I Giochi del Lunedì di Prisma tornano tra due settimane.