117. Giochi del 26 febbraio 2024 – Il Dilemma del Prigioniero, il Dilemma del Profeta e le strategie di cooperazione motivate da egoismo

I Giochi del Lunedì del 26 febbraio 2024 a cura di Fabio Ciuffoli 

Il Dilemma del Prigioniero è un classico della Teoria dei Giochi, che tratta scelte collaborative o competitive, con varie implicazioni: economiche, politiche, giuridiche, psicologiche e filosofiche. Di seguito presentiamo quattro problemi basati su questo interessante dilemma. Nel primo problema, due imprenditori turistici devono scegliere se rispettare o danneggiare l’ambiente. Il secondo problema analizza una sua possibile evoluzione. Nel terzo e nel quarto problema illustriamo un gioco proposto da Douglas Hofstadter sulle strategie di cooperazione motivate da egoismo e sulle strategie miste. Invitiamo i lettori a inviarci le loro considerazioni e proposte di soluzione utilizzando lo spazio riservato ai commenti. Domani alle ore 17.00 pubblicheremo le nostre soluzioni e le relative argomentazioni.

1. Il Dilemma del Prigioniero e la coimprenditorialità turistica

1. Due albergatori, A e B, possono decidere autonomamente tra due forme di utilizzazione dell’ambiente: rispettarlo (R) oppure danneggiarlo (D). Chi sceglierà la strategia del rispetto dell’ambiente dovrà sostenere maggiori costi (depuratori per non inquinare, spazi verdi, parcheggi auto attrezzati, ecc.). Chi sceglierà la strategia del danneggiamento, sfruttando in modo intensivo l’ambiente, non sosterrà costi aggiuntivi e di conseguenza avrà maggiori profitti. Nella tavola seguente sono indicate le quattro combinazioni di strategie, in ogni quadrante sono riportati i profitti in migliaia di euro dei due albergatori concorrenti: in alto a destra il profitto dell’albergatore A in rosso, in basso a sinistra quello dell’albergatore B in blu.

Il quadrante in alto a sinistra (20,20) indica il risultato della scelta di danneggiare sia di B che di A, il profitto di B è 20 e quello di A è 20. Il quadrante in alto a destra (70,10) indica che, se B danneggia l’ambiente mentre A  lo rispetta, i profitti di B sono 70 e quelli di A sono 10 e via di seguito. Ciascun albergatore può comunicare con l’altro, può mentire o essere leale, rispettare i patti oppure trasgredirli, come verosimilmente accade nella realtà.

1. Per ottenere il massimo profitto, quale strategia tra rispetto o danneggiamento dovrà adottare ciascun albergatore?

2. Il Dilemma del Profeta

Supponiamo che questo gioco sia ripetuto molte volte con un guadagno totale pari alla somma di tutti i giochi, come verosimilmente accade nella realtà. Un giocatore potrebbe “profetizzare” il comportamento dell’altro giocatore introducendo un fattore di ponderazione del rischio e ricalcolando i profitti, i giocatori potrebbero stipulare accordi e contratti con clausole punitive per chi non rispetta le regole e via di seguito.

2. Quale strategia adotterebbe l’albergatore B, se pensasse che anche l’albergatore A facesse le sue stesse scelte, supponiamo con un indice di fiducia del 90%?

2.1. Approfondimento. Sapreste calcolare l’indice di fiducia che rende indifferente la scelta dei due albergatori tra danneggiare o rispettare l’ambiente?

3. Strategie di cooperazione motivate da egoismo

Siamo sicuri che la cooperazione sia sempre e in ogni caso la miglior strategia?  Supponiamo di partecipare al seguente gioco (Gioco ideato da Douglas Hofstadter pubblicato su  “Scientic American”). Ad ogni concorrente viene sottoposta la seguente tabella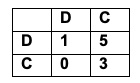I numeri rappresentano importi in dollari. I concorrenti possono essere due o più. Ogni concorrente può scegliere se disertare (D) o cooperare (C). Un ente esterno svolge il ruolo simbolico di “banco” e pagherà i premi ai singoli giocatori. I giocatori saranno premiati in base alle scelte degli altri partecipanti. Se diserti prendi 1$ per ognuno degli altri che diserta e 5$ per ciascuno degli altri che coopera. Se cooperi prendi 0 dollari per ciascuno degli altri che diserta e 3$ per ciascuno degli altri che coopera. Nessun concorrente può perdere in valore assoluto perché non ci sono numeri negativi . Ad esempio con due giocatori: se io diserto e anche l’altro diserta, io guadagno 1$ e l’altro giocatore guadagna 1$; se io diserto e l’altro coopera, io guadagno 5$ e l’altro guadagna zero; se io coopero e l’altro diserta, il mio guadagno è zero e l’altro prende 5$; se io coopero e l’altro coopera, il mio guadagno è 3$ e anche l’altro giocatore prende 3$.

Osservando la tabella, ogni giocatore ha una strategia dominante: disertare. Se diserta guadagna 1$ anziché zero oppure guadagna 5$ anziché 3$ a seconda delle scelte dell’altro.

In questo gioco i disertori fanno diminuire il guadagno medio di tutti i partecipanti, i cooperatori lo fanno salire. Il guadagno medio è dato dal seguente rapporto: tot. esborsi banco/n. partecipanti.

3. Se partecipassero 20 giocatori, quale sarebbe la strategia che permetterebbe il più alto valore del guadano medio?

4. Strategie miste

Ora ipotizziamo che i numeri e i segni, riportati in tabella, cambino e diventino quelli proposti di seguito.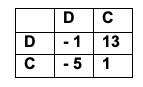

In questo caso vi sono numeri negativi, ciò vuol dire che i giocatori possono anche perdere e quindi pagare una somma al banco.  Ad esempio se tutti i venti partecipanti cooperassero, il banco sborserebbe 19$ e se tutti disertassero, incasserebbe 19$.

4. Quale strategia permette il maggior valore del guadagno medio? E come è possibile assegnare equamente i guadagni tra i partecipanti?

Aggiornamento per le soluzioni click qui.

Nell’immagine in evidenza una scena dal film A Beautful Mind del 2001.