
Soluzioni del 12 febbraio 2024 a cura di Fabio Ciuffoli
Ieri abbiamo presentato sei giochi tratti dall’interessante sito web di matematica ricreativa Mathigon. Di seguito pubblichiamo le nostre proposte di soluzione.
Mathigon: il parco giochi matematico
1. Con un solo taglio in linea retta dividere la forma di colore chiaro, disegnata nella figura seguente, in due pezzi per formare un quadrato.


2. Qual è la probabilità che la pallina, lasciata cadere dal vertice in alto nel labirinto di legno in figura, finisca nel contenitore B? Le palline possono muoversi solo verso il basso, quindi non rimbalzano e a ogni bivio hanno probabilità del 50% di andare a destra o a sinistra.
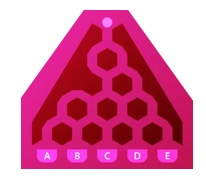
2. SOLUZIONE. La probabilità è 3/16. Ad esempio, provando 16 volte, 8 andranno su ciascun lato e così via fino al contenitore B che raccoglierà 3 palline. Per completezza, in ogni contenitore finiranno:
A. 0 palline (0%)
B. 3 palline (18,75%)
C. 7 palline (43,75%)
D. 5 palline (31,25%)
E. 1 pallina (6,25%)
3. Quale proporzione occupa l’acqua nella bottiglia in figura?
3. SOLUZIONE. L’acqua occupa i 2/3 della bottiglia. Immaginiamo che la bottiglia sia un cilindro. La figura a sinistra mostra che l'altezza dell'acqua dalla base sarebbe 10. La figura a destra mostra che l'altezza dell'aria dalla base sarebbe 5. Ciò significa che il cilindro con lo stesso volume della bottiglia ha altezza 15 e l’acqua occupa 10/15 = 2/3. 4. Qual è il rapporto tra le aree del triangolo e la “falce di luna”, disegnata in roso scuro, formata da due archi circolari?
4. SOLUZIONE. Chiamiamo r il raggio del quarto di cerchio che è anche il cateto del triangolo rettangolo isoscele e avremo:Area triangolo = r2/2.Con Pitagora calcoliamo l’ipotenusa che è anche il diametro del semicerchio ossia r√2. Ora calcoliamo l’area del semicerchio = π(r√2/2)2/2 che svolgendo diviene (2πr2/4)/2 = 2πr2/8.Calcoliamo l’aerea del segmento circolare, data dalla differenza tra area del quarto di cerchio meno area del triangolo: πr2/4 – r2/2 = (πr2 – 2r2)/4. Infine calcoliamo l’area della “falce di luna” come differenza tra area del semicerchio e area del segmento circolare: 2πr2/8 - (πr2 – 2r2)/4 svolgendo (2πr2 - (2πr2 – 4r2)/8 che diviene 4r2/8 semplificato r2/2. Sia il triangolo rettangolo che la "falce di luna" hanno esattamente la stessa area: il rapporto è 1.
5. Qual è l'area del semicerchio scuro collocato simmetricamente all'interno di un quarto di cerchio nella figura seguente?
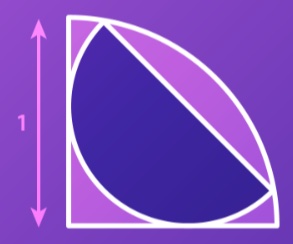
5. SOLUZIONE. Indichiamo con r il raggio del semicerchio e tracciamo due raggi per collegare il centro del semicerchio con i punti A e B, formando il quadrato OABC a sinistra nella figura seguente. Con Pitagora, la diagonale del quadrato, OC, ha lunghezza r√2. Tracciamo il raggio del quarto di cerchio OE e consideriamo il triangolo rettangolo OCE disegnato a destra in figura. Con Pitagora: 1 = r2 + (r√2)2 che diviene 1 = r2 + 2r2 poi 1 = 3r2 quindi r = √(1/3). L’area del semicerchio è (π/3)/2 = π/6.
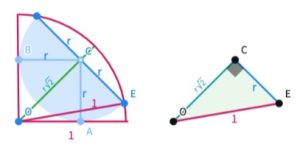
6. Un semicerchio è disposto all’interno un quadrato di lato 1 come proposto in figura seguente. Qual è il diametro del semicerchio?
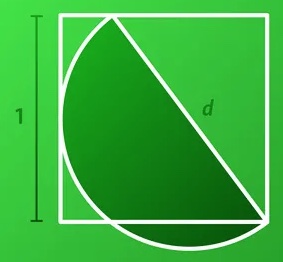
6. SOLUZIONE. Estendiamo il semicerchio per mostrare il cerchio completo e disegniamo il triangolo come in figura seguente. Il cerchio incontra il lato sinistro del quadrato al centro. L'angolo sinistro del triangolo è un angolo retto perché ogni punto di una circonferenza, collegato ai due estremi del diametro, forma un angolo retto. Il suo cateto maggiore è anche l’ipotenusa del triangolo rettangolo di lati 1 e ½ per cui misura √(5/4). A questo punto, applicando più volte Pitagora, avremo: d2 = a2 + (1/2)2 + 5/4 e d2 = (1 – a)2 + 1. Quindi a2 + 6/4 = 1 – 2a + a2 + 1 poi 2a = 2 – 6/4 = ½ infine a = ¼. Ora andando a sostituire avremo: d2 = 25/16, quindi d = 5/4.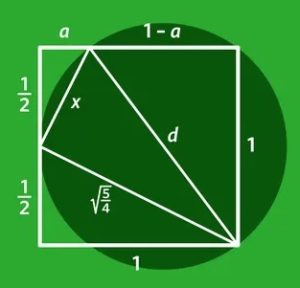
I Giochi del Lunedì tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).