115. Soluzioni del 29 gennaio 2024 – Equilibrio di impresa: massimizzare ricavi e profitti

Soluzioni del 29 gennaio 2024 a cura di Fabio Ciuffoli

Ieri mattina abbiamo presentato tre problemi classici di microeconomia con massimizzazione dei ricavi e degli utili in condizioni ideali di libera concorrenza e di monopolio. Di seguito pubblichiamo le nostre proposte di soluzione. 

Equilibrio di impresa: massimizzare ricavi e profitti – soluzioni 

1. Un negozio vende 50 kg di lamponi a settimana a € 25 al kg. Alcune ricerche di mercato indicano che per ogni riduzione del prezzo di € 2 al kg, la quantità venduta aumenterà di 5 kg a settimana. Se queste informazioni fossero attendibili, quale dovrebbe essere il prezzo al kg per massimizzare i ricavi settimanali?

1. SOLUZIONE. Indicando con p il nuovo prezzo al kg, con q la relativa quantità di kg venduta e con RS il conseguente  ricavo settimanale, avremo:

q = 50 + 5(25 – p)/2 = 112,5 – 2,5p

Possiamo calcolare il Ricavo Settimanale RS = p·q = p(112,5 – 2,5p) = 112,5p – 2,5p² e costruire la seguente tabella con il prezzo, la quantità e il ricavo settimanale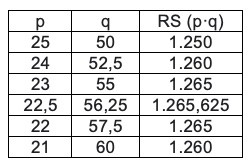Avremo il massimo RS quando il prezzo p = € 22,5 q = kg 56,25; RS = € 1.265,625. In sintesi se il prezzo viene ridotto a € 22,50 si avrà il ricavo settimanale massimo di € 1.265.625 con un aumento del ricavo di circa € 16 (1.265.625 – 1.250).

In forma algebrica, dall’equazione di secondo grado RS = 112,5p – 2,5p² determiniamo il massimo RS quando p =  (- b / 2a) = 112,5 / 5 = 22,5.

2. Un imprenditore produce farine alimentari. Il costo per materia prima e lavorazione è di € 32 al quintale, la spesa fissa mensile è di € 12.600. Determinare la quantità minima che deve produrre mensilmente per non essere in perdita e la quantità che permette il massimo utile, ipotizzando che ogni quantità prodotta sia venduta, nei due casi seguenti:

A. L’imprenditore opera in un mercato di concorrenza perfetta e vende il suo prodotto a € 52 al quintale;

B. L’imprenditore si trova in posizione monopolistica e la domanda in quintali è espressa dalla relazione q = 4.000 – 50p dove q è la quantità prodotta e venduta e p è il prezzo di vendita.

2. SOLUZIONE. Indichiamo con CF i cosi fissi, con cv i costi variabili unitari, con CV i costi variabili totali, con CT i costi totali, con q_e la quantità di equilibrio, con RT i ricavi totali e con U l’utile.

A. In condizioni ideali, di concorrenza perfetta, la quantità minima prodotta e venduta per non essere in perdita (quantità di equilibrio) è q_e = CF / (p – cv) = 12.600 / 52 – 32 = 630 q.li.

Sempre in condizioni di concorrenza perfetta, il massimo utile si avrà vendendo la quantità massima prodotta, che non viene specificata nel testo del problema. Ad esempio se ipotizziamo che la quantità massima sia 3.000 q.li, allora avremo

U_max = RT – CT = 52 · 3.000 – (12.600 + 32 · 3.000) = € 47.400.

Possiamo costruire la seguente tabella.

B. In condizione monopolistica: le quantità di equilibrio sono 300 q.li e 2.100 q.li con i prezzi rispettivamente di € 74 e € 38 euro al quintale. Il massimo ricavo è € 80.000 con prezzo € 40 al quintale, il massimo utile è € 16.200 con un prezzo di € 56 al quintale. Possiamo costruire la seguente tabella.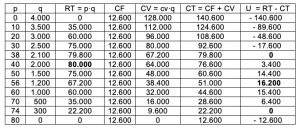In forma algebrica: a partire da q = 4.000 – 50p  determiniamo RT

RT = p·q = p(4.000 – 50p) = 4.000p – 50p².

Calcoliamo le quantità e i prezzi di equilibrio, ponendo RT = CT.

RT = CT  quindi p·q = (CF + cv·q) sostituendo 4.000p – 50p² = 12.600 + 32·(4.000 – 50p) che diviene 4.000p – 50p² = 12.600 + 128.000 – 1.600p. Otteniamo l’equazione di secondo grado: – 50p² + 5.600p – 140.600 = 0 con due soluzioni € 38 e € 74 che sono i due prezzi di equilibrio con le rispettive quantità di equilibrio q₁ = 2.100 q.li e q₂ = 300 q.li.

Calcoliamo il massimo ricavo a partire dall’equazione di secondo grado RT = 4.000p – 50p².

 Max RT = – b / 2a = 4.000 / 100 = 40. Il massimo ricavo si ottiene con un prezzo di € 40 al quintale producendo e vendendo una quantità di 2.000 q.li

Determiniamo ora il massimo utile U = RT – CT = p·q – (CF + cv·q) = 4.000p – 50p² – [12.600 + 32(4.000 – 50p)] = 4.000p – 50p² – 12.600 – 128.000 + 1.600p = – 50p² + 5.600p – 140.600.

Max U = – b / 2a = 5.600 / 100 = 56. Il massimo utile si ottiene con un prezzo di € 56 al quintale producendo e vendendo 1.200 q.li.

3. Un’impresa sostiene per la produzione di una merce: un costo fisso mensile di € 18.000; un costo per unità prodotta di € 160: un costo per la manutenzione degli impianti pari al 5% del quadrato del numero di unità prodotte. Vende la merce prodotta in condizioni di monopolio e la domanda è espressa dalla funzione: q = 4.000 – 10p dove q è la quantità prodotta e venduta e p è il prezzo di vendita. Determinare:

• A. la quantità da produrre e vendere di equilibrio con la quale i ricavi sono pari ai costi;
• B. la quantità da produrre e vendere per ottenere il massimo ricavo;
• C. la quantità da produrre e vendere per ottenere il massimo l’utile;
• D. la quantità di prodotti che permette il costo medio minimo.

3. SOLUZIONE. Indichiamo con CF i costi fissi, con cv i costi variabili unitari, con CV i costi variabili totali, con CT i costi totali, con c_m il costo medio, con q_e la quantità di equilibrio, con RT i ricavi totali e con U l’utile.

Le quantità di equilibrio sono 79 e 1.521 con i prezzi rispettivamente di € 392 e €248; il massimo ricavo è € 400.000 con prezzo € 200 e quantità 2.000; il massimo utile è € 78.000 con un prezzo di € 320 e quantità 800; il costo medio minimo è € 220 e con quantità prodotta 600.

Determiniamo in modo algebrico i risultati e di seguito li presentiamo in forma tabellare. Sappiamo che CF = 18.000; CV = 160q + 0,05q²; CT = 18.000 + 160q + 0,05q²; RT = p·q.

Partiamo da q = 4.000 – 10p  e lo trasformiamo in p = (4.000 – q)/10. Poi sostituiamo RT = p·q = p(4.000 – 10p) = 4.000p – 10p² oppure RT = [(4.000 – q)/10]q che diviene RT = (4.000q – q²)/10.

A) Calcoliamo le quantità e i prezzi di equilibrio, ponendo RT = CT che diviene pq = (CF + cv·q) sostituendo (4.000q – q²)/10= 18.000 + 160q + 0,05q²; svolgendo 4.000q – q² = 180.000 + 1.600q + 0,5q²; poi 1,5q² – 2.400q + 180.000 = 0. Dall’equazione di secondo grado avremo q₁ = 79 e q₂ = 1521 che sono le due quantità di equilibrio.

B) Calcoliamo il massimo ricavo a partire dall’equazione di secondo grado RT= 4.000p – 10p² e avremo Max RT = – b / 2a = 4.000 / 20 = 200. Il massimo ricavo si ottiene con un prezzo di € 200 producendo e vendendo quantità di 2.000.

C) Determiniamo ora il massimo utile a partire U = RT – CT che diviene U = pq – (CF + cv·q) = [(4.000q – q²)/10] – (18.000 + 160q + 0,05q²) = 4.000q – q² – 180.000 – 1.600q – 0,5q² = 1,5q² – 2.400q + 180.000. Dall’equazione di secondo grado determiniamo il Max U = – b / 2a = 2.400 / 3  = 800. Il massimo utile si ottiene con quantità 800 e prezzo € 320, quindi RT sarà € 256.000 e CT = € 178.000 per cui l’utile sarà di € 78.000.

D) Il costo medio è c_m = CT / q = (18.000 + 160q + 0,05q²) / q. E’ minimo quando la quantità prodotta è 600 e il c_m = € 220.

Infine presentiamo la seguente tabella.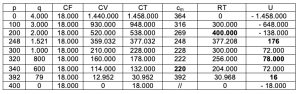

I Giochi del Lunedì di Prisma tornano tra due settimane.