109. Soluzione del 6 novembre 2023 – Accesso all’università in Corea del Sud

Soluzione del 6 novembre 2033 a cura di Fabio Ciuffoli

Ieri abbiamo presentato un difficile problema tratto dalle prove di accesso CSAT all’università in Corea del Sud e di seguito pubblichiamo la soluzione. Abbiamo diviso il procedimento in diverse fasi, ragionando gradualmente “passo passo” e, personalmente, ho trovato il racconto di questa soluzione una vera e propria narrazione avvincente! 

Accesso all’università in Corea del Sud

 Il disegno illustra una montagna a forma di cono circolare retta.

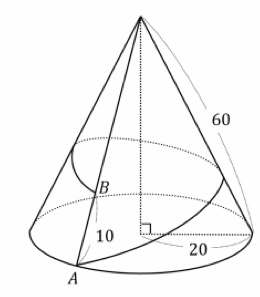
Si vuole costruire un binario con la distanza più breve possibile, per un treno panoramico, intorno alla montagna. Il binario inizia nel punto A e finisce nel punto B, il binario andrà prima in salita ma poi scenderà. Qual è la lunghezza del binario in discesa?

a. 200/√19       b. 300/√30       c. 300/√91       d. 400/√91

[Lunghezza lato obliquo del cono (apotema) = 60; raggio della circonferenza di base r = 20; segmento AB = 10].

Anche il problema è abbastanza difficile da capire, inoltre sembra contro-intuitivo che ci sia una parte del percorso in discesa. Problema molto difficile. La soluzione è sorprendente.

SOLUZIONE. Il primo passo è “srotolare” il cono e ottenere un settore circolare in modo da trasformare il problema da 3d in 2d, rendendo più facile la determinazione della distanza più breve tra A e B.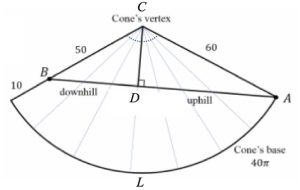

La soluzione procede in cinque fasi.

• 1. Trovare l’angolo al centro del settore circolare.
• 2. Posizionare i punti A e B sul settore circolare.
• 3. Calcolare la lunghezza di AB.
• 4. Identificare la parte in discesa di AB.
• 5. Calcolare la lunghezza della discesa.

1. Trovare l’angolo α al centro del settore circolare. La lunghezza dell’arco L coincide con la circonferenza della base del cono quindi L = 2πr = 40π. Il raggio del settore circolare è il lato obliquo del cono o apotema R = 60. Per calcolare l’angolo al centro del settore circolare α possiamo procedere in diversi modi, ad esempio calcolare la circonferenza di raggio 60 e metterla in relazione alla lunghezza dell’arco rapportandola poi a 360°.

2*60π / 40π che semplificato diviene 3π / π poi 

3π / π = 360°/ α  quindi  α = 120°.

2. Posizionare i punti A e B sul settore circolare. Posizioniamo il punto A su un angolo e il punto B sul raggio opposto dell’arco. Il punto B dista 10 unità dalla base e 50 unità dal vertice. Ora possiamo trovare il percorso più breve tra A e B tracciando il segmento tra i due punti. Questo crea un triangolo con i lati: AC, BC e AB. 

3. Calcolare la lunghezza AB. Ora possiamo determinare AB utilizzando la legge dei coseni¹, poiché abbiamo un triangolo con i lati 50, 60 e un angolo compreso di 120°.  

AB² = 60² + 50² – 2(60) (50) cos 120° = 9.100

AB = √ 9.100. 

(1) In un triangolo qualsiasi il quadrato di un lato é uguale alla somma dei quadrati degli altri due lati diminuita del doppio prodotto di questi due lati per il coseno dell’angolo che essi formano.

 4. Identificare la parte in discesa di AB. Il segmento AB indica prima una salita (distanza crescente dalla base/diminuzione distanza dal vertice) e poi una discesa (diminuzione distanza dalla base/distanza crescente dal vertice). Tra la parte in salita e in discesa c’è un punto su AB che è il più vicino al vertice del cono. La linea tra questo punto e il vertice del cono sarà perpendicolare ad AB, quindi si formano due triangoli rettangoli, con il cateto in comune h. 

5. Calcolare la lunghezza della pista in discesa. Sia x la lunghezza in discesa, quindi AB – x = √9.100 – x è la lunghezza in salita. Ora possiamo usare il teorema di Pitagora per i due triangoli rettangoli per ottenere:

• (√9100 – x)² + h² = 60²
• x² + h² = 50²

che diventano

• 9.100 + x² – 2√9100x + h² = 3.600
• x² + h² = 2.500

Ora ecco un bel trucco, sottraiamo la seconda equazione dalla prima. Quindi i termini x² e i termini h² si annullano e otteniamo:

9.100 – 2√9100x = 1.100  che diviene

2√9100x = 8.000 poi

x = 8.000 / 20√91 semplificando  x = 400/√91.

 Quindi questa è la risposta, la quarta tra quelle proposte. 

I Giochi del Lunedì tornano tra due settimane.