Menu
Le soluzioni del 23 ottobre 2023 a cura di Fabio Ciuffoli
Ieri abbiamo presentato tre giochi, che hanno fanno parte delle sfide matematiche settimanali per ragazzi di età dai 13 a 16 anni proposti durante l’anno scolastico alla King’s Maths School di Londra. Di seguito pubblichiamo le nostre proposte di soluzione.
Sfide matematiche alla King’s Math School – soluzioni
1. Sfere e cubi. Un cubo verde si trova all’interno di una sfera blu che tocca gli otto angoli del cubo. La sfera, a sua volta, si trova in un cubo giallo arancione che tocca i bordi della sfera, come disegnato in figura. Quante volte è maggiore il volume del cubo più grande, rispetto al volume del cubo più piccolo?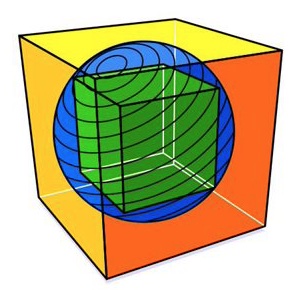
1. Soluzione. Definiamo la lunghezza del lato del cubo più piccolo 2a, in modo che a sia la lunghezza della metà di un lato del cubo piccolo in colore viola, nel disegno sotto, mentre X indica il centro del cubo. Ora calcoliamo la lunghezza del segmento verde, che coincide con il raggio della sfera blu.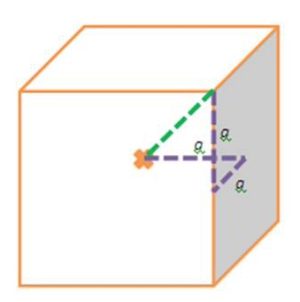
Abbiamo già definito la lunghezza del segmento viola con a, ora utilizzando il teorema di Pitagora due volte, troviamo la lunghezza del segmento verde che è a√3. [Prima applicazione Pitagora: a2 + a2 = 2a2 quindi ipotenusa √2a2 = a√2; seconda applicazione Pitagora: (a√2)2 + a2 = 2a2 + a2 = 3a2 quindi ipotenusa √3a2 = a√3 che è il raggio della sfera e metà del lato del cubo grande]. Notiamo che la lunghezza del segmento verde, ossia il raggio della sfera, è la metà del lato del cubo più grande giallo arancione, quindi il fattore di scala del lato, dal cubo piccolo al cubo grande, è √3. (circa 1,732) Il volume del cubo piccolo è (2a)3 e il volume del cubo grande è (2a√3)3. Pertanto il fattore di scala del volume, dal cubo più piccolo al cubo più grande, è (√3)3 = 3√3. In altri termini il volume del cubo più grande è 3√3 (circa 5,196) volte più grande del volume del cubo più piccolo.
2. Due scale. Il disegno seguente mostra due scale, posizionate tra due pareti, in modo che una scala raggiunga a metri sul muro di sinistra e l’altra scala raggiunga b metri sulla parete destra.
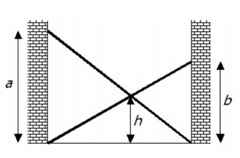Le due scale si incrociano ad un’altezza di h metri dal suolo. È possibile determinare h solo in termini di a e b, oppure abbiamo bisogno di conoscere altre misure, come la lunghezza tra i muri o la lunghezza delle scale?
2. Soluzione. Definiamo i punti sul terreno, toccati dalle frecce, rispettivamente A, H e B. Poiché il triangolo a sinistra con un lato = a e il triangolo a destra con un lato = b sono simili (in base alle regole degli angoli per le linee parallele) le altezze di questi due triangoli devono essere in rapporto a : b. Pertanto AH : HB = a : b quindi per qualche costante k, AH = ka, HB = kb e AB = k(a + b). Il triangolo rettangolo con base HB e altezza h è simile al triangolo rettangolo con base AB e altezza a, quindi confrontando i lati corrispondenti, h/kb = a/k(a + b) che semplificato diviene h = ab/(a + b) pertanto, per determinare h, non è necessario sapere la lunghezze delle scale o la distanza delle pareti.
3. La Torre Eiffel. A Parigi è una bellissima giornata limpida e ti trovi in cima alla Torre Eiffel. Quanto lontano puoi vedere? Più precisamente quanto dista, dalla parte inferiore della torre, il punto più lontano che puoi vedere sulla superficie della Terra? [Sappiamo che: l’altezza della Torre Eiffel è 301 m; il raggio della Terra è circa 6.371 km; si ipotizzano condizioni ideali, sfericità della Terra, visibilità, ecc.]
3. Soluzione. Disegniamo una tangente al cerchio (Terra) in modo che la cima della Torre Eiffel sia sulla continuazione della tangente e avremo un triangolo di lati:
Con Pitagora avremo: A2 + B2 = C2 quindi B = √ C2 – A2 ≈ 61,93 km. Tuttavia, poiché questa è la distanza visiva diretta dalla cima della Torre Eiffel e non dalla base, se volessimo calcolare la vera distanza dal suolo dovremmo calcolare la lunghezza dell’arco sulla superficie terrestre tra la base della Torre Eiffel e il punto più lontano del suo orizzonte. Utilizzando la trigonometria, calcoliamo l’angolo al centro della circonferenza (Terra) poi calcoliamo teoricamente l’arco di circonferenza.
I Giochi del Lunedì tornano tra due settimane.
In questa pagina vengono pubblicati giochi matematici, logici e di ragionamento ogni 15 giorni il lunedì in mattinata.
Siamo sempre alla ricerca di nuovi giochi e nuove proposte. Se vuoi suggerirne uno, scrivici un’e-mail a:
blog.giochi@prismamagazine.it
Fabio Ciuffoli è autore di diversi libri sul problem solving e i giochi logici e matematici, il più recente è Giochi matematici e logici.
PRISMA: pubblicazione mensile registrata presso il Tribunale di Milano (N. 235 del 19.09.2018).
Tutti i diritti di proprietà artistica e letteraria sono riservati.
L’editore è a disposizione di eventuali detentori di diritti che non sia stato possibile rintracciare.
Mateinitaly srl – p.iva 09164520968 – Corso Vercelli 27 – 20144 Milano (MI).